广东省广州市海珠区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是（）

A、0 B、 $\frac{1}{2}$ C、 $\sqrt{2}$ D、 $- 2$

查看试题解析
2. 若点 $P (2 ， a)$ 在第四象限，则a可以是（）

A、2 B、 $- 3$ C、0 D、1

查看试题解析
3. 下列调查适合抽样调查的是（）

A、某封控区全体人员的核酸检测情况 B、我国“天舟四号”航天飞船各零部件的质量情况 C、对旅客上飞机前的安全检查 D、一批节能灯管的使用寿命

查看试题解析
4. 若关于 $x$ ， $y$ 的方程 $m x - y = 1$ 的一个解是 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则m的值是（）

A、 $- 1$ B、1 C、3 D、 $- 3$

查看试题解析
5. 如果 $a > b$ ，那么下列各式中错误的是（）

A、 $a - 2 > b - 2$ B、 $\frac{a}{3} > \frac{b}{3}$ C、 $- 3 a > - 3 b$ D、 $5 a + 2 > 5 b + 2$

查看试题解析
6. 一个正方形的面积为32，则它的边长应在（）

A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间

查看试题解析
7. 在平面直角坐标系中，点P的坐标为 $(3 ， - 4)$ ，则点P到x轴的距离为（）

A、3 B、 $- 4$ C、 $- 3$ D、4

查看试题解析
8. 如图，将直尺与含30°角的直角三角尺摆放在一起，若 $∠ 2 = 125 °$ ，则 $∠ 1$ 的度数是（）

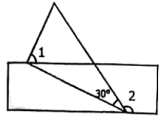A、65° B、35° C、30° D、25°

查看试题解析
9. 《九章算术》是中国传统数学最重要的著作，书中记载：“今有牛五、羊二、直金十二两；牛二、羊五、直金九两，问牛、羊各直金几何？”意思是：“假设有5头牛和2只羊共值金12两，2头牛和5只羊共值金9两．问每头牛、每只羊各值金多少两？”如果按书中记载，1头牛和1只羊一共值金（）两．

A、3 B、3.3 C、4 D、4.3

查看试题解析
10. 若不等式组 ${\begin{array}{l} x + 9 < 5 x + 1 \\ x > m \end{array}$ 的解集为 $x > 2$ ，则m的取值范围是（）

A、 $m \leq 2$ B、 $m < 2$ C、 $m \geq 2$ D、 $m > 2$

查看试题解析

二、填空题

11. 8的立方根为.

查看试题解析
12. 若 $x + 4 > 0$ ，则x的取值范围为．

查看试题解析
13. 将点 $A (2 ， - 1)$ 先向左平移1个单位，再向上平移3个单位，得到点 $A^{'}$ ，则点 $A^{'}$ 的坐标为．

查看试题解析
14. 某校食堂有甲、乙、丙三种套餐，为了解哪种套餐更受欢迎，学校调查了该校的全体学生，其中喜欢甲、乙、丙三种套餐的人数比为2∶5∶3，若选择甲套餐的有180名学生，则这个学校有名学生．

查看试题解析
15. 无论m取什么数，点 $(- 1 - m^{2} ， | m | + 1)$ 一定在第象限．

查看试题解析
16. 在平面直角坐标系中，某机器人从原点O出发，按向右，向上，向右，向下的方向每次移动1个单位长度，行走路线如图所示，第1次移动到 $A_{1} (1 ， 0)$ ，第2次移动到 $A_{2} (1 ， 1)$ ，第3次移动到 $A_{3} (2 ， 1)$ ，第4次移动到 $A_{4} (2 ， 0)$ …，则第2022次移动至点 $A_{2022}$ 的坐标是．

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{64} - \sqrt{{(- 3)}^{2}} + \sqrt[3]{- 27}$

(2)、 ${(- 1)}^{2022} + | \sqrt{3} - 2 | + 2 \sqrt{3}$

查看试题解析
18.

(1)、解方程组 ${\begin{array}{l} x + y = 10 \\ 2 x + y = 16 \end{array}$

(2)、解不等式组 ${\begin{array}{l} 3 x - 2 > 1 \\ x + 9 < 3 (x + 1) \end{array}$

查看试题解析
19. 三角形ABC（记作 $△ A B C$ ）在 $10 \times 10$ 方格中，位置如图所示，点A、点B的坐标分别为 $A (- 3 ， 2)$ ， $B (- 2 ， 4)$ ．

(1)、点C的坐标为；

(2)、把 $△ A B C$ 向上平移2个单位长度，再向右平移3个单位长度，得 $△ A_{1} B_{1} C_{1}$ ．请你画出平移后的 $△ A_{1} B_{1} C_{1}$ ；

(3)、求 $△ A B C$ 的面积．

查看试题解析
20. 如图，直线AB与CD相交于点O， $O E ⊥ C D$ ，垂足为O．

(1)、若 $∠ E O B = 40 °$ ，则 $∠ A O C =$ °；

(2)、若 $∠ B O E ： ∠ B O D = 2 ： 3$ ，求 $∠ B O C$ 的度数．

查看试题解析
21. 某中学决定开展课后托管服务，学校就“你最想开展哪种课后服务项目”问题进行了抽样问卷调查，调查分为四个类别：A．艺术、B．体育、C．科技、D．自主阅读．现根据调查结果整理并绘制成如下不完整的扇形统计图和条形统计图：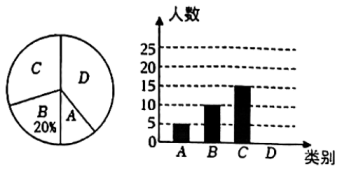

请结合图中所给信息解答下列问题

(1)、这次统计共抽查了名学生；

(2)、请补全条形统计图；

(3)、求扇形统计图中表示“C类别”的圆心角的度数；

(4)、该校共有1200名学生，根据以上信息，请你估计全校学生中想参加A类活动的有多少人？

查看试题解析
22. 有大小两种货车，3辆大货车和2辆小货车一次共运货17吨，6辆大货车和3辆小货车一次共运货31.5吨．

(1)、求每辆大货车和每辆小货车一次分别可以运货多少吨？

(2)、若要安排10辆货车运输至少35吨的货物，则至少安排多少辆大货车？

查看试题解析
23. 已知四边形ABCD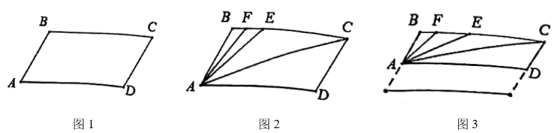， $B C ∥ A D$ ， $∠ B A D = ∠ B C D = 60 °$

(1)、如图1所示，求证： $A B ∥ C D$ ；

(2)、如图2所示，点E、F在线段BC上，且保持 $∠ D A C = ∠ E A C$ ， AF平分 $∠ B A E$ ．
①求证： $∠ B E A = 2 ∠ B C A$ ；
②如图3，若上下平行移动AD， $∠ A F B + ∠ A C D$ 的值是否发生变化？若变化，请说明理由；若不变，请求出它的值．

查看试题解析
24. 若平面直角坐标系上点P（x，y）的横、纵坐标满足关于x，y的方程组，则称点P为该方程组的关联点，如点N（2，1）为方程组 ${\begin{array}{l} 2 x - y = 3 \\ x + y = 3 \end{array}$ 的关联点．

(1)、若点E（1，2）为关于 $x$ ， $y$ 的方程组的 ${\begin{array}{l} 7 x - 2 y = a \\ 2 x - b y = 2 \end{array}$ 的关联点，则 $a =$ ， $b =$ ；

(2)、已知点A（x，y）为关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 7 x + 2 y = 1 \\ 2 x - y = 3 m - 2 \end{array}$ 的关联点，点B（x，y）为关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 2 x + y = - n + 3 \\ x - 2 y = 7 \end{array}$ 的关联点；若点A与点B重合，求点A的坐标，并求出 $m$ ， $n$ 的值；

(3)、已知 $P (x ， y)$ 为关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + 2 y = 3 m - 2 n - 5 \\ 2 x - y = m + n - 10 \end{array}$ 的关联点，若点P在第二象限，且符合条件的所有整数m之和为9，求n的范围．

查看试题解析
25. 在平面直角坐标系中，已知M（0，4），N（3，2），线段MN平移得到线段PQ，使点M的对应点为P，点N的对应点为Q，若点P的坐标为 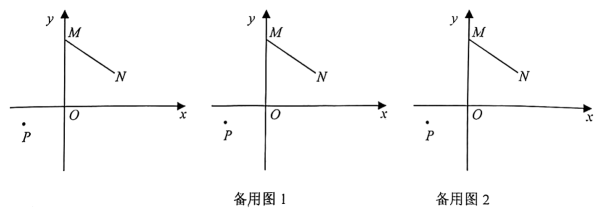$(- 2 ， - 1)$ ，点Q的坐标为 $(a ， b)$ ，

(1)、a= ， b=；

(2)、若点E为x轴正半轴上的一个动点，探究 $∠ M N E$ 、 $∠ N E Q$ 和 $∠ E Q P$ 之间的数量关系并证明；（注： $∠ M N E$ 、 $∠ N E Q$ 和 $∠ E Q P$ 均为大于 $0 °$ 且小于 $180 °$ 的角）

(3)、将线段MN向下平移得到线段AB，从使得点N的对应点B落在x轴上，点M的对应点A落在y轴上，动点C从点B出发，以每秒钟移动3个单位长度的速度沿x轴向左运动，动点D从点A出发，以每秒钟移动2个单位长度的速度沿y轴向下运动，直线BD与直线AC交于点F，设点F的坐标为 $(m ， n)$ ．动点C和动点D同时出发且它们的运动时间为t秒．
①在 $0 < t < 1$ 时，试探究 $△ A D F$ 与 $△ B C F$ 的面积关系，并说明理由；
②若在点C、D的运动过程中， $△ A B F$ 的面积为7，请直接写出m的值．

查看试题解析