广东省东莞市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-07-18 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在0,-1, , 2四个数中,最大的数是( )A、-1 B、0 C、 D、23. 下列各数中的无理数是( )A、 B、 C、0 D、4. 下列调查中,适宜采用抽样调查的是( )A、了解某校七年级(1)班学生的视力情况 B、调查某批次汽车的抗撞击能力 C、对与新冠肺炎患者在同一车厢的乘客进行核酸检测 D、调查天舟四号货运飞船各零部件的质量5. 不等式3x<6的解集在数轴上可表示为( )A、
 B、
B、 C、
C、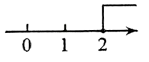 D、
D、 6. 如图,两条直线相交于一点,如果∠1+∠2=80°,则∠2的度数是( )
6. 如图,两条直线相交于一点,如果∠1+∠2=80°,则∠2的度数是( ) A、40° B、60° C、120° D、140°7. 已知是关于x,y的二元一次方程2x-y=m的一个解,则m的值是( )A、5 B、1 C、-1 D、-28. 若a>b,则下列式子中一定成立的是( )A、 B、 C、 D、9. 在平面直角坐标系中,如果过点A 和B的直线平行于x轴,且AB=4,则点B的坐标为( )A、 B、 C、或 D、或10. 如图, , 将一副直角三角板作如下摆放, , . 下列结论:①;②;③;④ . 其中正确的个数是( )
A、40° B、60° C、120° D、140°7. 已知是关于x,y的二元一次方程2x-y=m的一个解,则m的值是( )A、5 B、1 C、-1 D、-28. 若a>b,则下列式子中一定成立的是( )A、 B、 C、 D、9. 在平面直角坐标系中,如果过点A 和B的直线平行于x轴,且AB=4,则点B的坐标为( )A、 B、 C、或 D、或10. 如图, , 将一副直角三角板作如下摆放, , . 下列结论:①;②;③;④ . 其中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 9的算术平方根是 .12. 不等式组 的解集为 .13. 写出一个在x轴上点的坐标是 .14. 如图是九(1)班45名同学每周课外阅读时间的频数分布直方图(每组含前一个边界值。不含后一个边界值)。其中每周课外阅读时间在6小时及以上的人有名。
 15. 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD的度数为.
15. 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD的度数为. 16. 已知 , 则 .17. 如图,正方形ABCD的面积为3,点A在数轴上,且表示的数为-2,以点A为圆心,AB长为半径画弧,与数轴交于点E(点E在点A的右侧),则点E所表示的数为 .
16. 已知 , 则 .17. 如图,正方形ABCD的面积为3,点A在数轴上,且表示的数为-2,以点A为圆心,AB长为半径画弧,与数轴交于点E(点E在点A的右侧),则点E所表示的数为 .
三、解答题
-
18. 计算: .19. 解三元一次方程组:20. 在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
 (1)、将△ ABC先向下平移2个单位长度,再向右平移5个单位长度得到△ A1B1C1 , 画出△ A1B1C1 .(2)、求△ A1B1C1的面积.21. 2021年7月以来,教育部相继出台文件,实施义务教育“双减”政策,某校开展课后延时服务,从篮球、绘画、乐器、手工四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)、将△ ABC先向下平移2个单位长度,再向右平移5个单位长度得到△ A1B1C1 , 画出△ A1B1C1 .(2)、求△ A1B1C1的面积.21. 2021年7月以来,教育部相继出台文件,实施义务教育“双减”政策,某校开展课后延时服务,从篮球、绘画、乐器、手工四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题: (1)、在这次调查中,共调查了多少名学生?(2)、补全条形统计图.(3)、“绘画”所在扇形的圆心角是多少度?(4)、若该校爱好篮球的学生共有800名,则该校学生总数大约有多少名?22. 如图,已知∠AMB=∠GNB,∠CEA=∠FGB.
(1)、在这次调查中,共调查了多少名学生?(2)、补全条形统计图.(3)、“绘画”所在扇形的圆心角是多少度?(4)、若该校爱好篮球的学生共有800名,则该校学生总数大约有多少名?22. 如图,已知∠AMB=∠GNB,∠CEA=∠FGB. (1)、求证:;(2)、若∠ABD=∠D+40°,求∠D的度数.23. 2022年北京冬奥会和冬残奥会的吉样物分别是冰墩墩和雪容融,在某官方旗舰店购买1个冰墩墩和3个雪容融毛绒玩具需498元;购买2个冰墩墩和4个雪容融毛绒玩具需796元.(1)、求冰墩墩、雪容融毛绒玩具单价各是多少元?(2)、某单位准备用不超过3000元的资金在该官方旗舰店购进冰墩墩、雪容融两种毛绒玩具共20个,问最多可以购进冰墩墩毛绒玩具多少个?
(1)、求证:;(2)、若∠ABD=∠D+40°,求∠D的度数.23. 2022年北京冬奥会和冬残奥会的吉样物分别是冰墩墩和雪容融,在某官方旗舰店购买1个冰墩墩和3个雪容融毛绒玩具需498元;购买2个冰墩墩和4个雪容融毛绒玩具需796元.(1)、求冰墩墩、雪容融毛绒玩具单价各是多少元?(2)、某单位准备用不超过3000元的资金在该官方旗舰店购进冰墩墩、雪容融两种毛绒玩具共20个,问最多可以购进冰墩墩毛绒玩具多少个?
