北京市通州区2021-2022年七年级下学期期末数学试题
试卷更新日期:2022-07-18 类型:期末考试
一、单选题
-
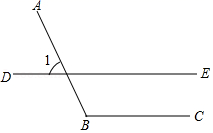
1. 某种芯片每个探针单元的面积为 ,0.00000164用科学记数法可表示为( )A、 B、 C、 D、2. 下列调查方式,你认为最合适的是( )A、对端午节期间市场上粽子质量情况,采用全面调查方式 B、旅客上飞机前的安检,采用抽样调查方式 C、调查本市居民对“垃圾分类”有关内容的了解程度,采用全面调查方式 D、调查“神舟十一号”飞船重要零部件的产品质量,采用全面调查方式3. 如图,已知DE∥BC,如果∠1=70°,那么∠B的度数为( )
 A、70° B、100° C、110° D、120°4. 下列式子从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、5. 以下命题是真命题的是( )A、相等的两个角一定是对顶角 B、过直线外一点有且只有一条直线与已知直线平行 C、两条直线被第三条直线所截,内错角相等 D、在同一平面内,垂直于同一条直线的两条直线互相垂直6. 已知二元一次方程的解,又是下列哪个方程的解( )A、 B、 C、 D、7. 在实数范围内规定新运算“”,其规则是: . 已知不等式的解集在数轴上如图表示,则的值是( )
A、70° B、100° C、110° D、120°4. 下列式子从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、5. 以下命题是真命题的是( )A、相等的两个角一定是对顶角 B、过直线外一点有且只有一条直线与已知直线平行 C、两条直线被第三条直线所截,内错角相等 D、在同一平面内,垂直于同一条直线的两条直线互相垂直6. 已知二元一次方程的解,又是下列哪个方程的解( )A、 B、 C、 D、7. 在实数范围内规定新运算“”,其规则是: . 已知不等式的解集在数轴上如图表示,则的值是( )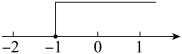 A、 B、0 C、1 D、28. 如图的网格线是由边长为1的小正方形格子组成的, 小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形,小明研究发现,内部含有3个格点的四边形的面积与该四边形边上的格点数有某种关系,请你观察图中的4个格点四边形.设内部含有3个格点的四边形的面积为S,其各边上格点的个数之和为 m,则S与m的关系为( )
A、 B、0 C、1 D、28. 如图的网格线是由边长为1的小正方形格子组成的, 小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形,小明研究发现,内部含有3个格点的四边形的面积与该四边形边上的格点数有某种关系,请你观察图中的4个格点四边形.设内部含有3个格点的四边形的面积为S,其各边上格点的个数之和为 m,则S与m的关系为( )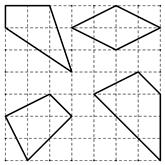 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
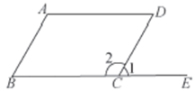
9. 分解因式: .10. 不等式 的正整数解是11. 若一个角的补角是其余角的3倍,则这个角的度数为 .12. 计算: .13. 把命题“等角的余角相等”改写成“如果…,那么…”的形式为 .14. 如图,点B、C、E在同一条直线上,请你写出一个能使成立的条件: . (只写一个即可,不添加任何字母或数字)
 15. 如图,在一个三角形三个顶点和中心处的每个“〇”中各填有一个式子,如果图中任意三个“〇”中的式子之和均相等,那么a的值为 .
15. 如图,在一个三角形三个顶点和中心处的每个“〇”中各填有一个式子,如果图中任意三个“〇”中的式子之和均相等,那么a的值为 .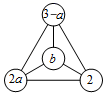 16. 为了测量一座古塔外墙底部的底角∠AOB的度数,李潇同学设计了如下测量方案:作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是 .
16. 为了测量一座古塔外墙底部的底角∠AOB的度数,李潇同学设计了如下测量方案:作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是 .
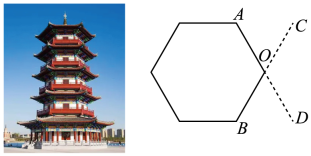 17. 某高校在“爱护地球,绿化祖国”的活动中,组织学生开展植树活动,为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据绘制成如图所示的统计图.那么这组数据的众数是棵,平均每人植树棵.
17. 某高校在“爱护地球,绿化祖国”的活动中,组织学生开展植树活动,为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据绘制成如图所示的统计图.那么这组数据的众数是棵,平均每人植树棵.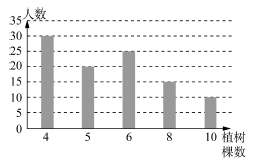 18. 手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如下:
18. 手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如下:工序
时间
模型
打磨(A组)
组装(B组)
模型1
9分钟
5分钟
模型2
6分钟
11分钟
则这两个模型都制作完成所需的最短时间为分钟.
三、解答题
-
19. 计算: .20. 解方程组21. 分解因式:(1)、;(2)、 .22. 已知3x2﹣x﹣1=0,求代数式(2x+5)(2x﹣5)+2x(x﹣1)的值.23. 解不等式组: ,并把它的解集在数轴上表示出来.
 24. 请在下列空格内填写结论或理由,完成推理过程.
24. 请在下列空格内填写结论或理由,完成推理过程.已知:如图, , .
求证: .
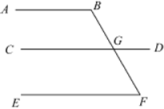
证明:∵(已知),
∴ ▲ // ▲ ( ).
∵(已知),
∴//( ).
∴// ▲ ( ).
∴( ).
25. 如图,三角形ABC中,过点C作于D,过点D作//交AC于点E.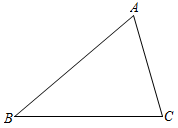 (1)、依题意,请补全图形;(2)、求证: .26. 疫情期间某学校储备“抗疫物资”,用8500元购进甲、乙两种医用口罩共计250盒,甲、乙两种口罩的售价分别是25元/盒,40元/盒.(1)、求甲、乙两种口罩各购进了多少盒?(2)、已知甲种口罩每盒50个、乙种口罩每盒100个,按照相关要求,学校必须储备足够使用10天的口罩,该校师生共计900人,每人每天2个口罩,问购买的口罩数量是否能满足要求.27. 一副三角板按如图放置,其中, , , , . 有下列说法:①如果 , 那么//;②如果// , 那么;③与的度数之和随着的变化而变化;④如果 , 那么 .
(1)、依题意,请补全图形;(2)、求证: .26. 疫情期间某学校储备“抗疫物资”,用8500元购进甲、乙两种医用口罩共计250盒,甲、乙两种口罩的售价分别是25元/盒,40元/盒.(1)、求甲、乙两种口罩各购进了多少盒?(2)、已知甲种口罩每盒50个、乙种口罩每盒100个,按照相关要求,学校必须储备足够使用10天的口罩,该校师生共计900人,每人每天2个口罩,问购买的口罩数量是否能满足要求.27. 一副三角板按如图放置,其中, , , , . 有下列说法:①如果 , 那么//;②如果// , 那么;③与的度数之和随着的变化而变化;④如果 , 那么 .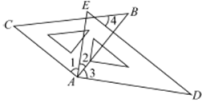 (1)、其中正确的是;(2)、请选择一个正确的加以证明.28. 某校初二年级有400名学生,为了提高学生的体育锻炼兴趣,体育老师自主开发了一套体育锻炼方法,并在全年级实施.为了检验此种方法的锻炼效果,随机抽取了20名学生在应用此种方法锻炼前进行了第一次体育测试,应用此种方法锻炼一段时间后,又进行了第二次体育测试,获得了他们的成绩(满分30分),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
(1)、其中正确的是;(2)、请选择一个正确的加以证明.28. 某校初二年级有400名学生,为了提高学生的体育锻炼兴趣,体育老师自主开发了一套体育锻炼方法,并在全年级实施.为了检验此种方法的锻炼效果,随机抽取了20名学生在应用此种方法锻炼前进行了第一次体育测试,应用此种方法锻炼一段时间后,又进行了第二次体育测试,获得了他们的成绩(满分30分),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.a.第一次体育测试成绩统计表:
分组/分
人数
1
1
9
3
b.第二次体育测试成绩统计图:
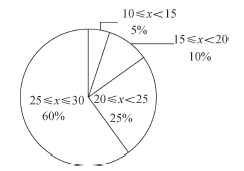
c.两次成绩的平均数、中位数、众数如下:
平均数
中位数
众数
第一次成绩
19.7
19
第二次成绩
25
26.5
28
d.第一次体育测试成绩在这一组的数据是:15,16,17,17,18,18,19,19,19.
e.第二次体育测试成绩在这一组的数据是:17,19.
请根据以上信息,回答下列问题:
(1)、m= , n=;(2)、第二次体育测试成绩为得分组所对应的圆心角度数是;第二次体育测试成绩的及格率(大于或等于18分为及格)为;(3)、下列推断合理的是 .①第二次测试成绩的平均分高于第一次的平均分,所以大多数学生通过此种方法锻炼一段时间后成绩都提升了.
②被抽测的学生小明的第二次测试成绩是24分,他觉得年级里大概有240人的测试成绩比他高.
29. 已知:直线 , 点G为直线CD上一定点 , 点E是直线AB上一动点 , 连结EG.在EG的左侧分别作射线EM、GN,两条射线相交于点F,设 .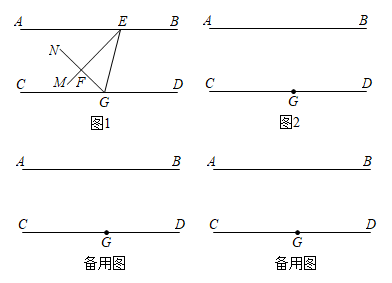 (1)、当 , 时,如图1位置所示,求的度数(用含有的式子表示),并写出解答过程;(2)、当时,过点G作EG的垂线 .
(1)、当 , 时,如图1位置所示,求的度数(用含有的式子表示),并写出解答过程;(2)、当时,过点G作EG的垂线 .①请在图2中补全图形;
②直接写出直线与直线CD所夹锐角的度数 ▲ (用含有的式子表示).