北京市海淀区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列数值是不等式 $x < 2$ 的解的是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 下面关于5与25关系的描述正确的是（）

A、 $5^{2} = 25$ B、 $5 = 2 5^{2}$ C、 $\sqrt{5} = 25$ D、 $\sqrt{25} = \pm 5$

查看试题解析
3. 下列命题是真命题的是（）

A、同位角相等 B、内错角相等 C、同旁内角互补 D、邻补角互补

查看试题解析
4. 如图，直线 $A B ∥ C D$ ， $C B$ 平分 $∠ A C D$ ， $∠ 1 = 50 °$ ，则∠2的度数是（）

A、50° B、55° C、60° D、65°

查看试题解析
5. 下列变形错误的是（）

A、由 $a > b$ 得 $a + 1 > b + 1$ B、由 $a > b$ 得 $a - 2 > b - 2$ C、由 $- 3 x > 3$ 得 $x > - 1$ D、由 $4 x > - 4$ 得 $x > - 1$

查看试题解析
6. 如图，数轴上，下列各数是无理数且表示的点在线段 $A B$ 上的是（）

A、0 B、 $\sqrt{2} - 1$ C、 $\sqrt[3]{- 9}$ D、 $π$

查看试题解析
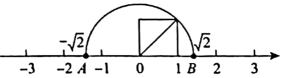7. 冰壶是在冰上进行的一种投掷性竞赛项日，被喻为冰上的“国际象棋”．右图是红、黄两队某局比赛投壶结束后冰壶的分布图，以冰壶大本营内的中心点为原点建立平面直角坐标系，按照规则更靠近原点的壶为本局胜方，则胜方最靠近原点的壶所在位置位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 方程组 ${\begin{array}{l} 2 x + y = 7 \\ x - y = 5 \end{array}$ ，的解满足的关系是（）

A、 $x - 2 y = 2$ B、 $x + 2 y = 2$ C、 $x + y = - 3$ D、 $x - y = 3$

查看试题解析
9. 已知 $a$ 是正数，下列关于 $x$ 的不等式组无解的是（）

A、 ${\begin{array}{l} x > a \\ x > 0 \end{array}$ B、 ${\begin{array}{l} x > a \\ x < 0 \end{array}$ C、 ${\begin{array}{l} x < a \\ x > 0 \end{array}$ D、 ${\begin{array}{l} x < a \\ x < 0 \end{array}$

查看试题解析
10. 下面是 $A ， B$ 两球从不同高度自由下落到地面后反弹高度的折线统计图，根据图中信息，在实验数据范围内，以下说法错误的是（）

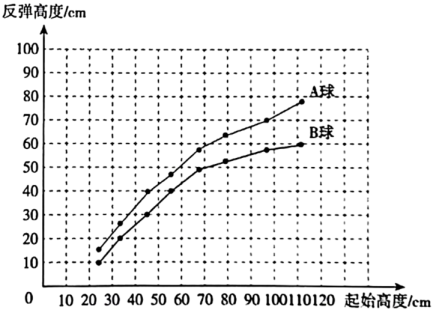A、 $A$ 球与 $B$ 球相比， $A$ 球的弹性更大 B、随着起始高度增加，两球的反弹高度也会增加 C、两球的反弹高度均不会超过相应的起始高度 D、将 $A$ 球从68cm的高度自由下落，第二次接触地面后的反弹高度小于40cm

查看试题解析

二、填空题

11. 图是对顶角量角器，用它测量角度的原理是．

查看试题解析
12. 计算： $3 \sqrt{3} - 2 \sqrt{3} =$ ．

查看试题解析
13. 如图是一家灯泡生产厂商的广告图，请从统计学角度判断广告语是否合适，并说明理由：

查看试题解析
14. 若关于x的方程 $2 x - 5 = a$ 的解为正数，则实数 $a$ 的取值范围是．

查看试题解析
15. 图1是面积为1的正方形，将其剪拼成如图2所示的三角形，剪拼前后图形面积．（填写“变大”，“变小”或“不变”）．

查看试题解析
16. 在平面直角坐标系 $x O y$ 中，若将点 $A$ 向左平移可得到点 $B (1 ， 2)$ ；若将点 $A$ 向上平移可得到点 $C (3 ， 4)$ ，则点 $A$ 的坐标是．

查看试题解析
17. 已知两个不相等的实数 $x ， y$ 满足： $x^{2} = a$ ， $y^{2} = a$ ，则 $\sqrt{x + y}$ 的值为．

查看试题解析
18. 埃拉托斯特尼是古希腊著名的地理学家，他曾巧妙估算出地球的周长．如图， $A$ 处是塞尼城中的一口深井，夏至日中午12时，太阳光可直射井底． $B$ 处为亚历山大城，它与塞尼城几乎司一条经线上，两地距离 $d$ 约为800km，于是地球周长可近似为 $\frac{360 °}{θ} \times d$ ，太阳光线看作平行光线，他在亚历山大城测得天顶方向与太阳光线的夹角 $α$ 为7.2°．根据 $α = 7.2 °$ 可以推导出 $θ$ 的大小，依据是；埃拉托斯特尼估算得到的地球周长约为km．

查看试题解析

三、解答题

19. 解方程组： ${\begin{array}{l} x - 2 y = 0 \\ 3 x - y = 5 \end{array}$

查看试题解析
20. 解不等式 $3 (2 x + 1) > 4 - 5$ ，并把解集在数轴上表示出来．

查看试题解析
21. 已知不等式 $x + 3 \leq 2 x + 5$ 与 $\frac{2 x + 4}{3} < 3 - x$ 同时成立，求 $x$ 的整数值．

查看试题解析
22. 如图，点 $A$ 在直线 $l$ 外，点 $B$ 在直线 $l$ 上，连接 $A B$ ．选择适当的工具作图．

(1)、在直线 $l$ 上作点 $C$ ，使 $∠ A C B = 90 °$ ，连接 $A C$ ；

(2)、在 $B C$ 的延长线上任取一点 $D$ ，连接 $A D$ ；

(3)、在 $A B$ ， $A C$ ， $A D$ 中，最短的线段是，依据是．

查看试题解析
23. 下图是北京冬奥会三个比赛场馆位置的平面示意图，图中小方格都是边长为1个单位长度的正方形，其中首都体育馆的坐标为（0，－2），国家速滑馆的坐标为（6，7）．

(1)、请在图中画出平面直角坐标系，并写出冰立方的坐标： ▲ ；

(2)、若五棵松体育中心的坐标为（－4，－6），请在坐标系中用点 $P$ 表示它的位置．

查看试题解析
24. 如图，已知 $∠ B A C = 90 °$ ， $D E ⊥ A C$ 于点 $H$ ， $∠ A B D + ∠ C E D = 180 °$ ．

(1)、求证： $B D ∥ E C$ ；

(2)、连接 $B E$ ，若 $∠ B D E = 30 °$ ，且 $∠ D B E = ∠ A B E + 50 °$ ，求 $∠ C E B$ 的度数．

查看试题解析

25. 清朝康熙年间编校的《全唐诗》包含四万多首诗歌，逾三百万字，是后人研究唐诗的重要资源．小云利用统计知识分析《全唐诗》中李白和杜甫作品的风格差异．下面给出了部分信息：

a．《全唐诗》中，李白和杜甫分别有896和1158首作品．

b．二人作品中与“风”相关的词语频数统计表如下：

词语

频数

诗人

春风

东风

清风

悲风

秋风

北风

李白

杜甫

c．通过统计二人的个性化用字，可绘制一种视觉效果更强的“词云图”，出现次数较多的关键字被予以视觉上的突出．

注：在文学作品中，东风即春风，常含有生机勃勃之意和喜春之情，如：等闲识得东风面，万紫千红总是春；北风通常寄寓诗人凄苦的情怀，抒写伤别之情，如：千里黄云白日曛，北风吹雁雪纷纷．

根据以上信息，回答下列问题：

(1)、补全条形统计图：

(2)、在与“风”相关的词语中，李白最常使用的词语是，大约每首诗歌中就会出现一次该词语（结果取整数），而杜甫最常使用的词语是；

(3)、下列推断合理的是．

①相较于杜甫，与“风”有关的词语在李白的诗歌中更常见；

②个性化用字中，李白最常使用的汉字是“水”，杜甫则是“江”；

③李白更常用“风”表达喜悦，而杜甫更常用“风”表达悲伤．

查看试题解析

26. 列方程（组）或不等式（组）解应用题：学校为了支持体育社团开展活动，鼓励同学们加强锻炼，准备增购一些羽毛球拍和乒乓球拍．

(1)、根据图中信息，求出每支羽毛球拍和每支乒乓球拍的价格；

(2)、学校准备用5300元购买羽毛球拍和乒乓球拍，且乒乓球拍的数量为羽毛球拍数量的3倍，请问最多能购买多少支羽毛球拍？

查看试题解析
27. 下图所示的格线彼此平行．小明在格线中作已知角，探究角的两边与格线形成的锐角所满足的数量关系．他先作出 $∠ A O B = 60 °$ ，

(1)、①如图1，点 $O$ 在一条格线上，当∠1＝20°时，∠2＝ ▲ °；
②如图2，点 $O$ 在两条格线之间，用等式表示∠1与∠2之间的数量关系，并证明；

(2)、在图3中，小明作射线 $O C$ ，使得 $∠ C O B = 45 °$ ．记 $O A$ 与图中一条格线形成的锐角为 $α$ ， $O C$ 与图中另一条格线形成的锐角为 $β$ ，请直接用等式表示α与B之间的数量关系．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于点 $A (x_{1} ， y_{1})$ ，点 $B (x_{2} ， y_{2})$ ，定义 $| x_{1} - x_{2} |$ 与 $| y_{1} - y_{2} |$ 中的值较大的为点 $A ， B$ 的“绝对距离”，记为 $d (A ， B)$ ．特别地，当 $| x_{1} - x_{2} | = | y_{1} - y_{2} |$ 时，规定 $d (A ， B) = | x_{1} - x_{2} |$ ，将平面内的一些点分为I，Ⅱ两类，每类至少包含两个点，记第I类中任意两点的绝对距离的最大值为 $d_{1}$ ，第Ⅱ类中任意两点的绝对距离的最大值为 $d_{2}$ ，称 $d_{1}$ 与 $d_{2}$ 的较大值为分类系数．如图，点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ 的横、纵坐标都是整数．

(1)、若将点 $A ， C$ 分为第I类，点 $B$ ， $D$ ， $E$ 分为第Ⅱ类，则 $d_{1} =$ ， $d_{2} =$ ，因此，这种分类方式的分类系数为；

(2)、将点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ 分为两类，求分类系数 $d$ 的最小值：

(3)、点 $F$ 的坐标为 $(m ， 2)$ ，已知将6个点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ 分为两类的分类系数的最小值是5，直接写出 $m$ 的取值范围．

查看试题解析