北京市丰台区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-07-18 类型:期末考试
一、单选题
-
1. 在下面四个关于“冰墩墩”的图形中,可以由右图经过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列调查方式,你认为最合适的是( )A、对某地区饮用水矿物质含量的调查,采用抽样调查方式 B、旅客上飞机前的安全检查,采用抽样调查方式 C、对某班学生的校服尺寸大小的调查,采用抽样调查方式 D、调查某批次汽车的抗撞击能力,采用全面调查方式3. 下列实数中为无理数的是( )A、 B、 C、 D、4. 下列命题中为假命题的是( )A、对顶角相等 B、两条平行线被第三条直线所截,同旁内角相等 C、在同一平面内,垂直于同一条直线的两条直线互相平行 D、如果两条直线都与第三条直线平行,那么这两条直线也互相平行5. 如图,直线DE过点A,且 .若 , ,则 的度数为( )
2. 下列调查方式,你认为最合适的是( )A、对某地区饮用水矿物质含量的调查,采用抽样调查方式 B、旅客上飞机前的安全检查,采用抽样调查方式 C、对某班学生的校服尺寸大小的调查,采用抽样调查方式 D、调查某批次汽车的抗撞击能力,采用全面调查方式3. 下列实数中为无理数的是( )A、 B、 C、 D、4. 下列命题中为假命题的是( )A、对顶角相等 B、两条平行线被第三条直线所截,同旁内角相等 C、在同一平面内,垂直于同一条直线的两条直线互相平行 D、如果两条直线都与第三条直线平行,那么这两条直线也互相平行5. 如图,直线DE过点A,且 .若 , ,则 的度数为( )
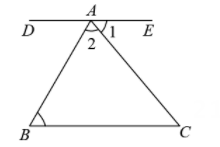 A、 B、 C、 D、6. 如果 , 那么下列不等式成立的是( )A、 B、 C、 D、7. 被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.书中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”原文大意为:“现在有5只雀、6只燕,分别集中放在天平上称重,聚在一起的雀重燕轻.将一只雀一只燕交换位置而放,重量相等,5只雀和6只燕共重1斤,问雀和燕各重多少?”设雀每只斤,燕每只斤,则可列出方程组为( )A、 B、 C、 D、8. 某学校组织初一学生去景区参加实践活动,学生张明和李华对着景区示意图(图中每个小正方形的边长均为)描述景点牡丹园的位置.张明说:“牡丹园的坐标是”,李华说“牡丹园在中心广场东北方向约处”.如果两人的说法都是正确的,根据以上信息,下列说法中错误的是( )
A、 B、 C、 D、6. 如果 , 那么下列不等式成立的是( )A、 B、 C、 D、7. 被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.书中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”原文大意为:“现在有5只雀、6只燕,分别集中放在天平上称重,聚在一起的雀重燕轻.将一只雀一只燕交换位置而放,重量相等,5只雀和6只燕共重1斤,问雀和燕各重多少?”设雀每只斤,燕每只斤,则可列出方程组为( )A、 B、 C、 D、8. 某学校组织初一学生去景区参加实践活动,学生张明和李华对着景区示意图(图中每个小正方形的边长均为)描述景点牡丹园的位置.张明说:“牡丹园的坐标是”,李华说“牡丹园在中心广场东北方向约处”.如果两人的说法都是正确的,根据以上信息,下列说法中错误的是( ) A、西门的坐标可能是 B、湖心亭的坐标可能是 C、中心广场在音乐台正南方向约处 D、南门在游乐园东北方向约处9. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“美学”.如图,的值接近黄金比 , 则黄金比( )(参考数据: , , , )
A、西门的坐标可能是 B、湖心亭的坐标可能是 C、中心广场在音乐台正南方向约处 D、南门在游乐园东北方向约处9. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“美学”.如图,的值接近黄金比 , 则黄金比( )(参考数据: , , , ) A、在0.1到0.3之间 B、在0.3到0.5之间 C、在0.5到0.7之间 D、在0.7到0.9之间10. 定义表示不超过实数的最大整数,例如: . 给出下列结论:
A、在0.1到0.3之间 B、在0.3到0.5之间 C、在0.5到0.7之间 D、在0.7到0.9之间10. 定义表示不超过实数的最大整数,例如: . 给出下列结论:①;
②若 , 则;
③若 , 则;
④若 , , 则 .
其中正确的个数是( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 的算术平方根是12. 已知是关于 , 的二元一次方程的解,则的值为 .13. 如图,点在射线上,请你添加一个条件 , 使得 .
 14. 某学校为调查学生对《中华人民共和国未成年人保护法》了解的情况,随机抽取部分学生进行调查,并将调查结果绘制成扇形统计图.如图,对该法“非常清楚”的学生对应扇形的圆心角度数为 .
14. 某学校为调查学生对《中华人民共和国未成年人保护法》了解的情况,随机抽取部分学生进行调查,并将调查结果绘制成扇形统计图.如图,对该法“非常清楚”的学生对应扇形的圆心角度数为 . 15. 关于x的不等式 解集是 ,写出一组满足a , b的值,a= , b= .16. 已知 , 是平面直角坐标系中的两点,这两点之间的距离的最小值为 .17. 某咖啡店提供三种咖啡,其对应两种容量的价格如下表所示:
15. 关于x的不等式 解集是 ,写出一组满足a , b的值,a= , b= .16. 已知 , 是平面直角坐标系中的两点,这两点之间的距离的最小值为 .17. 某咖啡店提供三种咖啡,其对应两种容量的价格如下表所示:咖啡品种
中杯()
大杯()
30元/杯
45元/杯
34元/杯
55元/杯
45元/杯
65元/杯
咖啡店开展回馈活动,凡自备容器购买咖啡者,每种中杯咖啡价格可减免2元、大杯咖啡价格可减免5元.
请根据上述信息,回答下列问题:
(1)、店长收到顾客反映,有的咖啡品种在自备容器后,同种大杯咖啡的每毫升价格还是比中杯的贵,请问是表中的品种(填“”,“”或“”);(2)、若要让所有咖啡品种在自备容器后,同种大杯咖啡的每毫升价格都比中杯的便宜,则应将大杯咖啡的价格至少减免元(减免的钱数为整数).18. 不等式的负整数解是 .三、解答题
-
19. 计算: .20. 解方程组: .21. 解不等式组:22. 补全解题过程.
已知:如图,于点 , 于点 , .
求证: .
证明:∵ , ,
∴ ▲ .
∴( )(填推理依据).
∴ ▲ ( )(填推理依据).
又∵ ,
∴ ▲ .
∴( )(填推理依据).
 23. 如图,在平面直角坐标系中,点 , , 过点作轴于点 .
23. 如图,在平面直角坐标系中,点 , , 过点作轴于点 .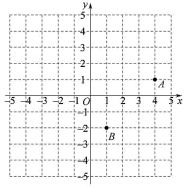 (1)、画出线段 , 并写出点的坐标;(2)、连接 , , 得到三角形 . 平移三角形 , 使得点与点重合,点 , 的对应点分别是 , , 画出三角形;(3)、直接写出三角形的面积.24. 科技改变世界,随着电子商务的高速发展,快递分拣机器人应运而生.某快递公司启用种机器人80台,种机器人100台,1小时共可以分拣8200件包裹;启用 , 两种机器人各50台,1小时共可以分拣4500件包裹.(1)、求 , 两种机器人每台每小时各分拣多少件包裹;(2)、快递公司计划再购进 , 两种机器人共200台.若要保证购进的这批机器人每小时的总分拣量不少于9000件,求最多应购进种机器人的台数.25. 某学校为了合理地安排学生体育锻炼,需要掌握学生每天课后进行体育锻炼时间的大致情况.在4月份某天随机抽取了若干名学生进行调查,发现被调查的学生当天课后进行体育锻炼的时间都不超过100分钟.现将调查结果绘制成两幅尚不完整的统计图表.
(1)、画出线段 , 并写出点的坐标;(2)、连接 , , 得到三角形 . 平移三角形 , 使得点与点重合,点 , 的对应点分别是 , , 画出三角形;(3)、直接写出三角形的面积.24. 科技改变世界,随着电子商务的高速发展,快递分拣机器人应运而生.某快递公司启用种机器人80台,种机器人100台,1小时共可以分拣8200件包裹;启用 , 两种机器人各50台,1小时共可以分拣4500件包裹.(1)、求 , 两种机器人每台每小时各分拣多少件包裹;(2)、快递公司计划再购进 , 两种机器人共200台.若要保证购进的这批机器人每小时的总分拣量不少于9000件,求最多应购进种机器人的台数.25. 某学校为了合理地安排学生体育锻炼,需要掌握学生每天课后进行体育锻炼时间的大致情况.在4月份某天随机抽取了若干名学生进行调查,发现被调查的学生当天课后进行体育锻炼的时间都不超过100分钟.现将调查结果绘制成两幅尚不完整的统计图表.课后体育锻炼时间频数分布表
组别
锻炼时间(分钟)
频数(学生人数)
百分比
12
20%
35%
18
6
10%
3
5%

根据以上信息,回答下列问题:
(1)、直接写出本次调查的样本容量,以及频数分布表中 , 的值;(2)、补全频数分布直方图;(3)、若该校学生共有2200人,估计该校当天课后体育锻炼时间超过60分钟的学生人数.26. 阅读下列材料:如图1, , , 分别是 , 上的点,点在 , 之间,连接 , . 用等式表示 , 与的数量关系.
小刚通过观察,实验,提出猜想: .
接着他对猜想的结论进行了证明,证明思路是:
过点作 , 由 , 可得 , 根据平行线的性质,可得 , , 从而证得 .

请你利用小刚得到的结论或解题思路,完成下列问题.
已知 , , 分别是 , 上的点,点在 , 之间,连接 , .
(1)、如图2,若 , , 则的度数为;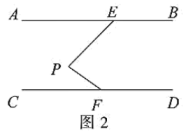 (2)、如图3,与的平分线交于点 , 用等式表示与的数量关系,并证明;
(2)、如图3,与的平分线交于点 , 用等式表示与的数量关系,并证明; (3)、如图4,与的平分线交于点 , 直接用等式表示与的数量关系.
(3)、如图4,与的平分线交于点 , 直接用等式表示与的数量关系.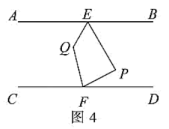 27. 在平面直角坐标系中,对于任意两点 , , 定义为点和点的“阶距离”,其中 . 例如:点 , 的“阶距离”为 . 已知点 .
27. 在平面直角坐标系中,对于任意两点 , , 定义为点和点的“阶距离”,其中 . 例如:点 , 的“阶距离”为 . 已知点 . (1)、若点 , 求点和点的“阶距离”;(2)、若点在轴上,且点和点的“阶距离”为4,求点的坐标;(3)、若点 , 且点和点的“阶距离”为1,直接写出的取值范围.
(1)、若点 , 求点和点的“阶距离”;(2)、若点在轴上,且点和点的“阶距离”为4,求点的坐标;(3)、若点 , 且点和点的“阶距离”为1,直接写出的取值范围.