2022年陕西省初中数学真题模拟试题汇编专题3 一次函数

试卷更新日期：2022-07-17 类型：二轮复习

进入出卷网下载

一、单选题

1. 在同一平面直角坐标系中，直线 $y = - x + 4$ 与 $y = 2 x + m$ 相交于点 $P (3 ， n)$ ，则关于x，y的方程组 ${\begin{array}{l} x + y - 4 = 0 \\ 2 x - y + m = 0 \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = - 1 \\ y = 5 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 9 \\ y = - 5 \end{array}$

查看试题解析
2. 若正比例函数的图象经过不同象限的两点A（a，2）和B（3，b），则一次函数y＝ax+b的图象所经过的象限是（　　）

A、一、二、三 B、二、三、四 C、一、二、四 D、一、三、四

查看试题解析
3. 已知一次函数 $y = k x + b (k \neq 0)$ ，函数值y随自变量x的增大而减小，且 $k + b > 0$ ，则函数 $y = k x + b$ 的图象经过的象限是（）

A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限

查看试题解析
4. 一次函数 $y = k x + b (k < 0)$ 的图象过点 $(- 1 ， 0)$ ，则不等式 $k x + b > 0$ 的解集是（）

A、 $x < - 2$ B、 $x < - 1$ C、 $x > - 2$ D、 $x < 1$

查看试题解析
5. 在同一平面直角坐标系中，直线 $y = k x - 3$ 是由直线 $y = 2 x + b$ 经过平移得到的，则下列各点在直线 $y = k x - 3$ 上的是（）

A、 $(- 2 ， 1)$ B、 $(1 ， - 2)$ C、 $(3 ， 3)$ D、 $(5 ， 13)$

查看试题解析
6. 若函数y＝kx＋b由直线y＝－x＋2平移得到，且平移后的直线过点（2，1），则直线y＝kx＋b与y轴的交点坐标是（）

A、（0，－3） B、（3，0） C、（1，2） D、（0，3）

查看试题解析
7. 已知点A（﹣3，﹣2）沿水平方向向右平移4个单位长度得到点A'.若点A'在直线y＝x+b上，则b的值为（）

A、5 B、3 C、1 D、﹣3

查看试题解析
8. 已知点A（2，y₁）和点B（a，y₂）在一次函数y＝﹣3x﹣b的图象上，且y₁＞y₂ ，则a的值可能是（）

A、3 B、0 C、﹣1 D、﹣2

查看试题解析
9. 在平面直角坐标系中，将直线l₁：y＝3x－2平移后得到直线l₂：y＝3x＋4，则下列平移方法正确的是（）

A、将l₁向上平移2个单位长度 B、将l₁向上平移4个单位长度 C、将l₁向左平移2个单位长度 D、将l₁向右平移3个单位长度

查看试题解析
10. 已知直线 $l_{1}$ 经过点 $(- 1 ， - 4)$ ，直线 $l_{2}$ 经过点 $(- 1 ， 0)$ ，若 $l_{1}$ 与 $l_{2}$ 关于 $y$ 轴对称，则 $l_{1}$ 、 $l_{2}$ 与 $x$ 轴围成的三角形面积为（）

A、1 B、2 C、3 D、4

查看试题解析

二、综合题

11. 如图，是一个“函数求值机”的示意图，其中y是x的函数.下面表格中，是通过该“函数求值机”得到的几组x与y的对应值.

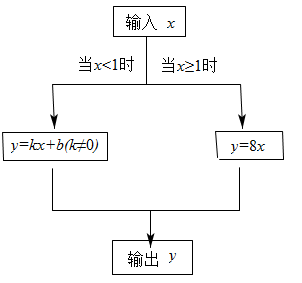
输人x	…	-6	-4	-2	0	2	…
输出y	…	-6	-2	2	6	16	…

根据以上信息，解答下列问题：

(1)、当输入的x值为1时，输出的y值为；

(2)、求k，b的值；

(3)、当输出的y值为0时，求输入的x值.

查看试题解析

12. 习近平总书记指出：“考古是一项重要文化事业，也是一项具有重大社会政治意义的工作.”百年考古，成就辉煌；国家使命，陕西担当.近日，全国首座考古学科专题博物馆——陕西考古博物馆于西安正式建成，开始对外试行开放.小张期待已久，提前预约门票，骑自行车去离家20千米的考古博物馆参观，其离家的距离y（千米）随骑行时间x（时）变化的图象（全程）如图所示.

(1)、小张出发0.25小时，离家的距离是千米；

(2)、求出AB所在直线的函数关系式；

(3)、出发1.5小时，小张距终点还有多少千米？

查看试题解析
13. 某生物小组观察一植物生长，得到植物高度y（单位：厘米）与观察时间x（单位：天）的关系，并画出如图所示的图象（AC是线段，直线CD平行x轴）.

(1)、该植物从观察时起，多少天以后停止长高？

(2)、求直线AC的解析式，并求该植物最高长多少厘米？

查看试题解析
14. 陕西省某游乐园推出了两种收费方式.
方式一：顾客先购买月卡，每张月卡120元，仅限两名家长和一名儿童当月使用，凭卡游玩，不限游玩次数，每人每次只需付5元.

方式二：顾客不购买月卡，每次游玩，每个成年人付费20元，每个儿童付费15元.

设一名顾客带着他的妻子和6岁孩子，在一个月内来此游乐园的次数为x次，设选择方式一的总费用为 $y_{1}$ （元），选择方式二的总费用为 $y_{2}$ （元）.

(1)、请分别写出 $y_{1}$ ， $y_{2}$ 与x之间的函数表达式.

(2)、该顾客一个月内在此游乐园游玩的次数x在什么范围时，选择方式一比方式二省钱.

查看试题解析

15. “相约西安，筑梦全运”，2021年9月15日至27日，第十四届全运会在陕西西安举行.小明一家开车去观看比赛，将油箱加满油后进行了油耗试验，得到如下数据：

轿车行使路程x（km）	0	10	20	30	40	…
油箱剩余油量y（1）	50	49.3	48.6	47.9	47.2	…

(1)、根据上表数据，求邮箱剩余油量y（1）与轿车行使的路程x（km）之间的函数关系式；

(2)、小明将油箱加满后，驾车从家到西安，到达西安时剩余油量为29L，求小明家到西安的距离？若小明一家返回途中，最多可行驶多少千米？（精确到个位）

查看试题解析

16. 甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发开向乙地.如图，线段OA表示货车离甲地距离y（km）与时间x（h）之间的函数关系；折线BCD表示轿车离甲地距离y（km）与x（h）之间的函数关系.

请根据图象，解答下列问题：

(1)、求线段CD对应的函数表达式；

(2)、求货车从甲地出发后多长时间与轿车相遇？

查看试题解析
17. 随着人民生活水平的提高，环境污染问题日趋严重，为了更好治理和净化河道，保护环境，河道综合治理指挥部决定购买10台污水处理设备．现有 $A$ 、 $B$ 两种型号的设备，其中 $A$ 型号设备的价格为12万元 $/$ 台，每月可处理污水220吨， $B$ 型号设备的价格为10万元 $/$ 台，每月可处理污水180吨，设购买 $A$ 型设备 $x$ 台， $A$ 、 $B$ 两种型号的设备每月总共能处理污水 $y$ 吨．

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、由于受资金限制，河道综合治理指挥部决定购买污水处理设备的总资金不超过110万元，问每月最多能处理污水多少吨？

查看试题解析
18. 某年级430名师生秋游，计划租用8辆客车，现有甲、乙两种型号客车，它们的载客量和租金如下表：

甲种客车
乙种客车
载客量（座/辆）
60
45
租金（元/辆）
550
450

(1)、设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；

(2)、当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？

查看试题解析

	甲种客车	乙种客车
载客量（座/辆）	60	45
租金（元/辆）	550	450