2022年陕西省初中数学真题模拟试题汇编专题2 方程与不等式

试卷更新日期：2022-07-17 类型：二轮复习

进入出卷网下载

一、单选题

1. 一次函数 $y = k x + b (k < 0)$ 的图象过点 $(- 1 ， 0)$ ，则不等式 $k x + b > 0$ 的解集是（）

A、 $x < - 2$ B、 $x < - 1$ C、 $x > - 2$ D、 $x < 1$

查看试题解析
2. 已知函数 $y = a x^{2} - (a + 1) x + 1$ ，则下列说法正确的个数是（）
①若该函数图象与x轴只有一个交点，则 $a = 0$

②方程 $a x^{2} - (a + 1) x + 1 = 0$ 有一个整数根是1

③存在实数a，使得 $a x^{2} - (a + 1) x + 1 \geq 0$ 对任意实数x都成立

A、0 B、1 C、2 D、3

查看试题解析
3. 用配方法解一元二次方程 $x^{2} - 6 x - 5 = 0$ ，下列变形正确的是（）

A、 ${(x - 6)}^{2} = - 5 + 36$ B、 ${(x - 6)}^{2} = 5 + 36$ C、 ${(x - 3)}^{2} = - 5 + 9$ D、 ${(x - 3)}^{2} = 5 + 9$

查看试题解析

二、填空题

4. 实数a，b在数轴上对应点的位置如图所示，则a $- b$ .（填“>”“=”或“<”）

查看试题解析
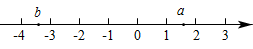5. 若关于x的一元二次方程 $x^{2} + x + m^{2} - 1 = 0$ 的一个根为－1，则m的值是．

查看试题解析
6. 已知 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} - 4 x + 2 = 0$ 的两个实数根，则 $x_{1} + x_{2} =$ .

查看试题解析
7. 若n边形内角和是外角和的3倍，则n=.

查看试题解析
8. 已知关于x的一元二次方程mx²﹣4x+2＝0有两个不相等的实数根，则m的取值范围是 .

查看试题解析
9. 《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1，图2所示，图中各行从左到右列出的算筹数分别表示未知数 $x ， y$ 的系数与相应的常数项．把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来，就是 ${\begin{array}{l} 3 x + 2 y = 19 \\ x + 4 y = 23 \end{array}$ ．类似地，图2所示的算筹图我们可以表述为．

查看试题解析
10. 我国明代数学读本《算法统宗》中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托．问：索子与竿子分别长多少托？若设索子长 $x$ 托，竿子长 $y$ 托，则列方程组为．

查看试题解析
11. 某地2021年3月份接种新冠病毒疫苗的有1万人次，5月份接种新冠病毒疫苗的有1.21万人次，从3月份到5月份，该地接种新冠病毒疫苗人次平均每月的增长率．

查看试题解析
12. 已知反比例函数 $y = \frac{1 - 3 m}{x}$ 的图象上两点 $A (- 3 ， y_{1})$ ， $B (1 ， y_{2})$ .若 $y_{1} < y_{2}$ ，则m的取值范围是.

查看试题解析

三、计算题

13. 解方程： $\frac{2}{x - 3} - \frac{x - 1}{3 - x} = 2$

查看试题解析
14. 解不等式组： ${\begin{array}{l} x + 2 > - 1 \\ x - 5 ⩽ 3 (x - 1) \end{array}$

查看试题解析
15. 解不等式组： ${\begin{array}{l} x + 4 > - 2 x + 1 ， \\ \frac{x}{2} - \frac{x - 1}{3} \leq 1 . \end{array}$

查看试题解析

四、解答题

16. 解不等式组： ${\begin{matrix} 2 x + 5 \leq 3 (x + 2) \\ \frac{x - 1}{2} < 1 \end{matrix}$ ，并把解集在数轴上表示出来.

查看试题解析
17. 李优用172元买了甲、乙两种书共10本，甲种书每本18元，乙种书每本10元，李优买甲、乙两种书各多少本？

查看试题解析
18. 解不等式 $\frac{2 x + 1}{4} \leq \frac{x - 1}{3} + 1$ ，并写出它的非负整数解

查看试题解析
19. 中国是最早发现并利用茶的国家，形成了具有独特魅力的茶文化，每年5月21日为国际茶日.紫阳毛尖和午子仙毫是我省两个著名的茶叶品种.某茶庄一周内紫阳毛尖和午子仙毫的销售总额为54000元，已知紫阳毛尖的单价1000元/千克，午子仙毫的单价600元/千克，紫阳毛尖的销售量比午子仙毫少10克.求这家茶庄一周内紫阳毛尖和午子仙毫的销量分别是多少千克？

查看试题解析
20. 开展农技培训，实施人才强村战略，因地制宜采用新媒体手段远程指导生产，利用广播电视、微信公众号等开展农技培训.某地区加强了培训经费的投入，2020年投入3000万元，预计2022年投入4320万元.求该地区这两年投入培训经费的年平均增长率.

查看试题解析

五、综合题

21. 五一期间，甲、乙两家樱桃采摘园的品质相同，销售价格也相同，销售价格均为每千克20元，两家均推出了不同的优惠方案，甲采摘园的优惠方案是：游客进园需购买50元的门票，采摘的樱桃六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘的樱桃不超过10千克则按原价购买，超过部分五折优惠.优惠期间，设某游客的樱桃采摘量为x（千克），在甲采摘园所需总费用为y₁（元），在乙采摘园所需总费用为y₂（元）.

(1)、甲采摘园优惠后的樱桃销售价格是每千克元；

(2)、求y₁、y₂与x的函数表达式；

(3)、当采摘樱桃在什么范围内时，在甲采摘园更优惠.

查看试题解析

22. 某校为改善办学条件，计划购进A、B两种规格的书架，经市场调查发现有线下和线上两种购买方式，具体情况如表：

规格	线下		线上
规格	单价（元/个）	运费（元/个）	单价（元/个）	运费（元/个）
A	240	0	210	20
B	300	0	250	30

(1)、如果在线上购买A、B两种书架20个，共花费y元，设其中A种书架购买x个，求y关于x的函数关系式；

(2)、在（1）的条件下，若购买B种书架的数量不少于A种书架的2倍，请求出花费最少的购买方案，并计算按照这种购买方案线上比线下节约多少钱.

查看试题解析

23. 张伯伯家专业种植狗头枣，他利用直播销售方式把狗头枣远销全国各地.对狗头枣出售价格根据购买量给予优惠，设顾客一次性购买狗头枣 $x kg$ ，付款y元，y与x之间的函数关系如图所示.

(1)、求y与x之间的函数关系式；

(2)、某位顾客通过直播在张伯伯家一次性购买狗头枣共花费870元，这位顾客共购买了多少千克狗头枣？

查看试题解析
24. 小王计划从某批发市场批量购买A、B两种仿古秦兵马俑工艺品摆件，已知A种摆件的批发价比B种摆件的批发价每个少5元，且用400元购买的A种摆件数量与用500元购买的B种摆件数量相同．

(1)、求A、B两种摆件的单价各是多少？

(2)、凭会员卡在此批发市场购买商品可以获得8折优惠，会员卡费用为50元，若小王购买会员卡并用此卡按需购买100个仿古秦兵马俑工艺品摆件，共用了y元，设A种摆件购买了x个，请求出y与x之间的函数关系式．若小王共用了1930元，则他购买A、B两种摆件各多少个？

查看试题解析
25. 香香猪肉铺10月五花肉售价约30元/千克，后受市场供需关系影响，五花肉价格逐月上涨，12月五花肉售价约为36.3元/千克，若在此期间五花肉价格每月增长率相同．

(1)、求此期间五花肉价格月增长率．

(2)、11月某天小刚妈妈用99元在香香猪肉铺买了一些五花肉包饺子，请问她买了多少五花肉．

查看试题解析
26. 为了进一步丰富校园活动，学校准备购买一批足球和篮球，购买2个篮球和3个足球共需425元，购买3个篮球和4个足球所花的钱一样多.

(1)、求篮球和足球的单价各是多少？

(2)、若学校购买15个篮球8个足球共需多少元？

查看试题解析
27. 有两张长12cm，宽10cm的矩形纸板，分别按照图1与图2两种方式裁去若干小正方形和小矩形，剩余部分（阴影部分）恰好做成无盖和有盖的长方体纸盒各一个.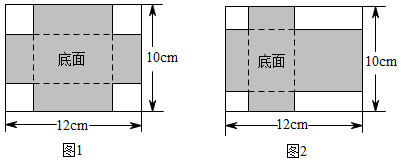

(1)、做成有盖长方体纸盒的裁剪方式是（填“图1”或“图2”）.

(2)、已知图1中裁去的小正方形边长为1.5cm，求做成的纸盒的底面积.

(3)、已知按图2裁剪方式做成纸盒的底面积为24cm² ，则剪去的小正方形的边长为多少cm？

查看试题解析