陕西省中考数学历年(2016-2022年)真题分类汇编专题8 四边形
试卷更新日期:2022-07-17 类型:二轮复习
一、单选题
-
1. 在下列条件中,能够判定为矩形的是( )A、 B、 C、 D、2. 如图,在菱形 中, ,连接 、 ,则 的值为( )
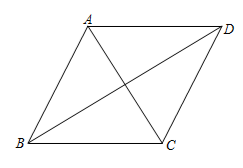 A、 B、 C、 D、3. 如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )
A、 B、 C、 D、3. 如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )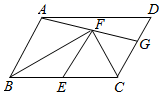 A、 B、 C、3 D、24. 如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF,则下列结论正确的是( )
A、 B、 C、3 D、24. 如图,在菱形ABCD中,点E,F,G,H分别是边AB,BC,CD和DA的中点,连接EF,FG,GH和HE,若EH=2EF,则下列结论正确的是( ) A、AB= EF B、AB=2EF C、AB= EF D、AB= EF5. 如图,在矩形ACBO中,A(-2,0),B(0,1).若正比例函数y=kx的图像经过点C,则k的取值为( )
A、AB= EF B、AB=2EF C、AB= EF D、AB= EF5. 如图,在矩形ACBO中,A(-2,0),B(0,1).若正比例函数y=kx的图像经过点C,则k的取值为( ) A、- B、 C、-2 D、26. 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
A、- B、 C、-2 D、26. 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( ) A、 B、 C、 D、7.
A、 B、 C、 D、7.如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
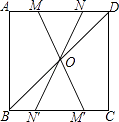 A、2对 B、3对 C、4对 D、5对8. 如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )
A、2对 B、3对 C、4对 D、5对8. 如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )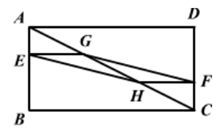 A、1 B、 C、2 D、4
A、1 B、 C、2 D、4二、填空题
-
9. 正九边形一个内角的度数为.10. 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个多边形的一个外角为45°,则这个正多边形的边数是 .
B.运用科学计算器计算:3 sin73°52′≈ . (结果精确到0.1)
11. 如图,在正五边形ABCDE中,DM是边CD的延长线,连接BD,则∠BDM的度数是.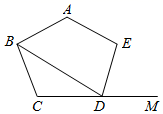 12. 如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.
12. 如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为. 13. 点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF= AB;G、H分别是BC边上的点,且GH= BC;若S1 , S2分别表示∆EOF和∆GOH的面积,则S1 , S2之间的等量关系是
13. 点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF= AB;G、H分别是BC边上的点,且GH= BC;若S1 , S2分别表示∆EOF和∆GOH的面积,则S1 , S2之间的等量关系是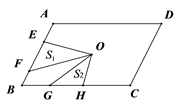 14. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF= .
14. 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,AC的中点,点F是AD的中点.若AB=8,则EF= .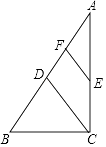 15.
15.如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 .
 16. 如图,在菱形中,.若M、N分别是边上的动点,且 , 作 , 垂足分别为E、F,则的值为.
16. 如图,在菱形中,.若M、N分别是边上的动点,且 , 作 , 垂足分别为E、F,则的值为.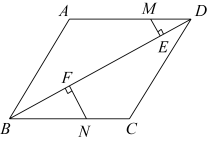 17. 如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6. P为对角线BD上一点,则PM—PN的最大值为.
17. 如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6. P为对角线BD上一点,则PM—PN的最大值为. 18. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 .
18. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为 .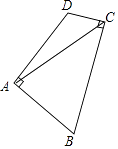
三、解答题
-
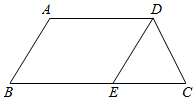
19. 如图,在四边形ABCD中,AD∥BC,∠B=∠C.E是边BC上一点,且DE=DC.求证:AD=BE.
 20. 如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE交于点G.求证:AG=CG.
20. 如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE交于点G.求证:AG=CG. 21.
21.问题提出
 (1)、如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.
(1)、如图①,已知△ABC,请画出△ABC关于直线AC对称的三角形.问题探究
(2)、如图②,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决
(3)、如图③,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG= 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积;若不能,请说明理由.22. 问题提出: (1)、如图1,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;
(1)、如图1,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;问题探究:
(2)、如图2,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离;问题解决:
(3)、如图3,有一座草根塔A,按规定,要以塔A为对称中心,建一个面积尽可能大的形状为平行四边形的草根景区BCDE。根据实际情况,要求顶点B是定点,点B到塔A的距离为50米,∠CBE=120°,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE?若可以,求出满足要求的平行四边形BCDE的最大面积;若不可以,请说明理由。(塔A的占地面积忽略不计)