陕西省中考数学历年（2016-2022年）真题分类汇编专题5 二次函数

试卷更新日期：2022-07-17 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知抛物线y=﹣x²﹣2x+3与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{5}}{5}$ D、2

查看试题解析
2. 已知抛物线y=x²﹣2mx﹣4（m＞0）的顶点M关于坐标原点O的对称点为M′，若点M′在这条抛物线上，则点M的坐标为（）

A、（1，﹣5） B、（3，﹣13） C、（2，﹣8） D、（4，﹣20）

查看试题解析
3. 对于抛物线y＝ax²＋(2a－1)x＋a－3，当x＝1时，y＞0，则这条抛物线的顶点一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 已知二次函数y=x²−2x−3的自变量x₁ ， x₂ ， x₃对应的函数值分别为y₁ ， y₂ ， y₃.当−1<x₁<0，1<x₂<2，x₃>3时，y₁ ， y₂ ， y₃三者之间的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
5. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值：

$x$

…

-2

0

1

3

…

$y$

…

6

-4

-6

-4

…

下列各选项中，正确的是

A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于-6 D、当 $x > 1$ 时，y的值随x值的增大而增大

查看试题解析
6. 在平面直角坐标系中，将抛物线y＝x²﹣（m﹣1）x+m（m＞1）沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 在同一平面直角坐标系中，若抛物线 $y = x^{2} + (2 m - 1) x + 2 m - 4$ 与 $y = x^{2} - (3 m + n) x + n$ 关于y轴对称，则符合条件的m，n的值为（）

A、m= $\frac{5}{7}$ ,n= $- \frac{18}{7}$ B、m=5，n= -6 C、m= -1，n=6 D、m=1，n= -2

查看试题解析

二、综合题

8.
如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax²+bx+5经过点M（1，3）和N（3，5）

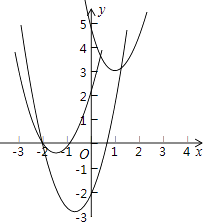(1)、试判断该抛物线与x轴交点的情况；

(2)、平移这条抛物线，使平移后的抛物线经过点A（﹣2，0），且与y轴交于点B，同时满足以A、O、B为顶点的三角形是等腰直角三角形，请你写出平移过程，并说明理由．

查看试题解析
9. 在同一直角坐标系中，抛物线C₁：y=ax²﹣2x﹣3与抛物线C₂：y=x²+mx+n关于y轴对称，C₂与x轴交于A，B两点，其中点A在点B的左侧．

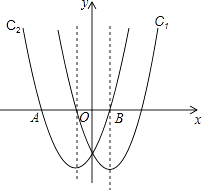(1)、求抛物线C₁ ， C₂的函数表达式；

(2)、求A，B两点的坐标；

(3)、在抛物线C₁上是否存在一点P，在抛物线C₂上是否存在一点Q，使得以AB为边，且以A，B，P，Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．

查看试题解析
10. 现要修建一条隧道，其截面为抛物线型，如图所示，线段 $O E$ 表示水平的路面，以O为坐标原点，以 $O E$ 所在直线为x轴，以过点O垂直于x轴的直线为y轴，建立平面直角坐标系.根据设计要求： $O E = 10 m$ ，该抛物线的顶点P到 $O E$ 的距离为 $9 m$ .

(1)、求满足设计要求的抛物线的函数表达式；

(2)、现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到 $O E$ 的距离均为 $6 m$ ，求点A、B的坐标.

查看试题解析
11. 已知抛物线 $y = - x^{2} + 2 x + 8$ 与x轴交于点A、B（其中A在点B的左侧），与y轴交于点C.

(1)、求点B、C的坐标；

(2)、设点 $C^{'}$ 与点C关于该抛物线的对称轴对称在y轴上是否存在点P，使 $△ P C C^{'}$ 与 $△ P O B$ 相似且 $P C$ 与 $P O$ 是对应边？若存在，求点P的坐标；若不存在，请说明理由.

查看试题解析
12. 如图

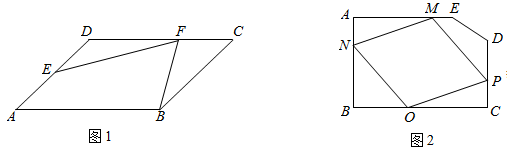(1)、问题提出
如图1，在 $▱ A B C D$ 中， $∠ A = 45 °$ ， $A B = 8$ ， $A D = 6$ ，E是 $A D$ 的中点，点F在 $D C$ 上且 $D F = 5$ 求四边形 $A B F E$ 的面积.（结果保留根号）

(2)、问题解决
某市进行河滩治理，优化美化人居生态环境.如图2所示，现规划在河畔的一处滩地上建一个五边形河畔公园 $A B C D E$ 按设计要求，要在五边形河畔公园 $A B C D E$ 内挖一个四边形人工湖 $O P M N$ ，使点O、P、M、N分别在边 $B C$ 、 $C D$ 、 $A E$ 、 $A B$ 上，且满足 $B O = 2 A N = 2 C P$ ， $A M = O C$ .已知五边形 $A B C D E$ 中， $∠ A = ∠ B = ∠ C = 90 °$ ， $A B = 800 m$ ， $B C = 1200 m$ ， $C D = 600 m$ ， $A E = 900 m$ .满足人工湖周边各功能场所及绿化用地需要，想让人工湖面积尽可能小.请问，是否存在符合设计要求的面积最小的四边形人工湖 $O P M N$ ？若存在，求四边形 $O P M N$ 面积的最小值及这时点 $N$ 到点 $A$ 的距离；若不存在，请说明理由.

查看试题解析
13. 已知抛物线L：y＝x²＋x－6与x轴相交于A、B两点（点A在点B的左侧），并与y轴相交于点C．

(1)、求A、B、C三点的坐标，并求出△ABC的面积；

(2)、将抛物线向左或向右平移，得到抛物线L´，且L´与x轴相交于A´、B´两点（点A´在点B´的左侧），并与y轴交于点C´，要使△A´B´C´和△ABC的面积相等，求所有满足条件的抛物线的函数表达式．

查看试题解析
14. 如图，抛物线y＝x²+bx+c经过点（3，12）和（﹣2，﹣3），与两坐标轴的交点分别为A，B，C，它的对称轴为直线l.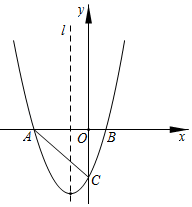

(1)、求该抛物线的表达式；

(2)、P是该抛物线上的点，过点P作l的垂线，垂足为D，E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等，求满足条件的点P，点E的坐标.

查看试题解析
15. 在平面直角坐标系中，已知抛物线L： $y = a x {}^{2}+ (c - a) x + c$ 经过点A（-3，0）和点B（0，-6），L关于原点O对称的抛物线为 $L^{'}$ .

(1)、求抛物线L的表达式；

(2)、点P在抛物线 $L^{'}$ 上，且位于第一象限，过点P作PD⊥y轴，垂足为D.若△POD与△AOB相似，求符合条件的点P的坐标.

查看试题解析

$x$	…	-2	0	1	3	…
$y$	…	6	-4	-6	-4	…