（人教版）2022-2023学年度第一学期七年级数学4.1.2 点、线、面、体 同步测试
试卷更新日期：2022-07-17 类型：同步测试
一、单选题
-
1. 将下列图形绕直线l旋转一周，可得圆锥的是（ ）A、
B、
C、
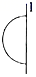D、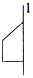
2. 在一个有盖的正方体玻璃容器内装了一些水（约占一半），把容器按不同方式倾斜，容器内水面的形状不可能是（ ）
A、
B、
C、
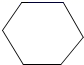D、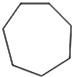
3. 如图，将一个直角三角形绕它的一条直角边所在的直线旋转一周，得到的几何体是圆锥，这一现象能用以下哪个数学知识解释（ ）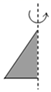
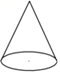A、点动成线 B、线动成面 C、面动成体 D、面面相交得线4. 用一个平面去截一个几何体，截面是圆，这个几何体可能是（ ）A、五棱柱 B、圆柱 C、长方体 D、棱锥5. 用一个平面截一个正方体，截面形状不可能是（ ）A、三角形 B、四边形 C、五边形 D、七边形6. 如图，5个边长为 的立方体摆在桌子上，则露在表面的部分的面积为（ ）
A、 B、 C、 D、7. 用一个平面去截下列立体图形，截面可以得到三角形的立体图形有（ ）
A、1个 B、2个 C、3个 D、4个8. 从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图5所示的零件，则这个零件的表面积是（ ）
A、20 B、22 C、24 D、269. 下列说法正确的是（ ）①正方体的截面可以是等边三角形；②正方体不可能截出七边形；③用一个平面截正方体，当这个平面与四个平面相交时，所得的截面一定是正方形；④正方体的截面中边数最多的是六边形
A、①②③④ B、①②③ C、①③④ D、①②④10. 如图，四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体中截面不可能是长方形的几何体是（ ）A、
B、
C、
D、
二、填空题
-
11. 用一个平面去截五棱柱，则截面不可能的一个图形是 ．
①三角形；②四边形；③五边形；④圆（将正确的序号填上即可）．
12. 电视剧《西游记》中，孙悟空的“金箍棒”飞速旋转，形成一个圆面，这说明（请填入符合题意答案的序号）．①点动成线；②线动成面；③面动成体．
13. 用一个平面截一个几何体，截面中有圆，这个几何体可以是.（写一个即可）14. 如图，三棱柱的底面边长都为2 cm，侧棱长为5 cm，则这个三棱柱的侧面展开图的面积为 ．
15. 用平面去截球体与圆柱，如果得到的截面形状相同，那么截面的形状是 ．三、解答题
-
16. 小学时，有一道趣味数学题：“稀奇稀奇真稀奇，4刀切成9块瓜，吃完剩下10块皮”，今天你能画图解释一下吗？17. 如图，截一个正方体，可以得到三角形，但要得到一个最大的等边三角形，你会切吗？你能说出你的切法吗？
18. 如图是一个长为4cm，宽为3cm的长方形纸片，该长方形纸片分别绕长、宽所在直线旋转一周（如图1、图2），会得到两个几何体，请你通过计算说明哪种方式得到的几何体的体积大（结果保留π）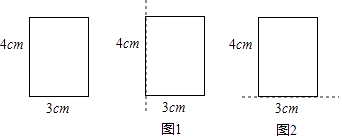
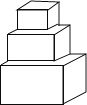
19. 在一个长方形中，长和宽分别为4cm、3cm，若该长方形绕着它的一边旋转一周，形成的几何体的体积是多少？（结果用π表示）20. 将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，现有一个长是5cm、宽是6cm的长方形，分别绕它的长、宽所在的直线旋转一周，得到不同的圆柱几何体，它们的体积分别是多大？21.有3个棱长分别是3cm，4cm，5cm的正方体组合成如图所示的图形．其露在外面的表面积是多少？（整个立体图形摆放在地上）
22.从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体，得到一个如图的零件，求：
（1）这个零件的表面积（包括底面）；
（2）这个零件的体积．
