(沪教版)2022-2023学年度第一学期九年级数学26.3 二次函数y=ax2+bx+c的图像 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
1. 已知二次函数y=ax2+bx+c(a≠0,a,b,c为常数),如果a>b>c,且a+b+c=0,则它的图象可能是( )A、
 B、
B、 C、
C、 D、
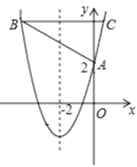
D、 2. 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
2. 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( ) A、1.4 B、2.5 C、2.8 D、33. 某二次函数的图象与函数y= x2﹣4x+3的图象形状相同、开口方向一致,且顶点坐标为(﹣2,1),则该二次函数表达式为( )A、y= (x﹣2)2+1 B、y= (x﹣2)2﹣1 C、y= (x+2)2+1 D、y=﹣ (x+2)2+14. 与抛物线 关于 轴对称的抛物线的解析式为( )
A、1.4 B、2.5 C、2.8 D、33. 某二次函数的图象与函数y= x2﹣4x+3的图象形状相同、开口方向一致,且顶点坐标为(﹣2,1),则该二次函数表达式为( )A、y= (x﹣2)2+1 B、y= (x﹣2)2﹣1 C、y= (x+2)2+1 D、y=﹣ (x+2)2+14. 与抛物线 关于 轴对称的抛物线的解析式为( ) A、 B、 C、 D、5. 如图,已知抛物线 与 轴分别交于 、 两点,将抛物线 向上平移得到 ,过点 作 轴交抛物线 于点 ,如果由抛物线 、 、直线 及 轴所围成的阴影部分的面积为 ,则抛物线 的函数表达式为( )
A、 B、 C、 D、5. 如图,已知抛物线 与 轴分别交于 、 两点,将抛物线 向上平移得到 ,过点 作 轴交抛物线 于点 ,如果由抛物线 、 、直线 及 轴所围成的阴影部分的面积为 ,则抛物线 的函数表达式为( ) A、 B、 C、 D、6. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法中,错误的是( )
A、 B、 C、 D、6. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法中,错误的是( ) A、对称轴是直线x= B、当﹣1<x<2时,y<0 C、a+c=b D、a+b>﹣c7. 抛物线 y=-2x2+8x-5 的对称轴是( )A、x=2 B、x=-2 C、x=4 D、x=-48. 二次函数y=﹣2x2+4x+3的图象的顶点坐标是( )A、(1,5) B、(﹣1,5) C、(1,3) D、(﹣1,3)9. 已知二次函数y=2 ﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有 , , 三点满足 =m,则m的值是( )A、1 B、 C、2 D、410. 二次函数y = x2-2x-3的图象如图所示,则函数值y<0时,x的取值范围是( )
A、对称轴是直线x= B、当﹣1<x<2时,y<0 C、a+c=b D、a+b>﹣c7. 抛物线 y=-2x2+8x-5 的对称轴是( )A、x=2 B、x=-2 C、x=4 D、x=-48. 二次函数y=﹣2x2+4x+3的图象的顶点坐标是( )A、(1,5) B、(﹣1,5) C、(1,3) D、(﹣1,3)9. 已知二次函数y=2 ﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有 , , 三点满足 =m,则m的值是( )A、1 B、 C、2 D、410. 二次函数y = x2-2x-3的图象如图所示,则函数值y<0时,x的取值范围是( )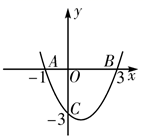 A、-1<x<3 B、x<-1 C、x>3 D、x<-1或 x>3
A、-1<x<3 B、x<-1 C、x>3 D、x<-1或 x>3二、填空题
-
11. 二次函数y=ax2+bx+c图象上部分点的坐标满足下表:
x
…
-3
-2
-1
0
1
…
y
…
-3
-2
-3
-6
-11
…
则该函数图象的顶点坐标为
12. 若点(m,0)在二次函数y=x2﹣3x+2的图象上,则2m2﹣6m+2029的值为 .13. 已知二次函数的图像经过原点,则a的值是 .14. 二次函数的对称轴为 .15. 抛物线 ( )的对称轴为 ,经过点(1,n),顶点为P,下列四个结论:①若 ,则 ;
②若c与n异号,则抛物线与x轴有两个不同的交点;
③方程 一定有两个不相等的实数解;
④设抛物线交y轴于点C,不论a为何值,直线PC始终过定点(3,n).
其中正确的是(填写序号).
三、解答题
-
16. 二次函数y=ax2+bx+c的图象经过点A(4,0),B(0,﹣3),C(﹣2,0),求它的解析式,直接写出它的开口方向、对称轴和顶点坐标.17. 已知抛物线(b是常数)经过点.求该抛物线的解析式和顶点坐标.18. 已知点(0,3)在二次函数 的图象上,且当 时,函数 有最小值2,这个二次函数的表达式。19. 在等式中,当时,;当时,;时,.求、、的值.20. 求下列二次函数图象的对称轴和顶点坐标: .21. 若二次函数y=ax2+bx+c的图象的顶点是(2,1)且经过点(1,2),求此二次函数解析式.