（沪教版）2022-2023学年度第一学期九年级数学25.4 解直角三角形的应用同步测试

试卷更新日期：2022-07-16 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，明年舟山将再添一个最高颜值城市新地标，新城长峙岛上将矗立起一座摩天轮，其直径为90m，旋转1周用时15min．小明从摩天轮的底部（与地面相距0.5m）出发开始观光，摩天轮转动1周，小明在离地面68m以上的空中有多长时间？（）

A、3min B、5min C、6min D、10min

查看试题解析
2. 如图，电线杆 $C D$ 的高度为h，两根拉线 $A C$ 与 $B C$ 相互垂直， $∠ C A B = θ$ ，则拉线 $B C$ 的长度为（A、D、B在同一条直线上）（）

A、 $\frac{h}{s i n θ}$ B、 $\frac{h}{c o s θ}$ C、 $\frac{h}{t a n θ}$ D、 $h ⋅ c o s θ$

查看试题解析
3. 如图，给出了一种机器零件的示意图，其中 $C E = 1$ 米， $B F = \sqrt{3}$ 米，则 $A B =$ （）

A、 $(1 + \sqrt{3})$ 米 B、 $(\sqrt{3} - 1)$ 米 C、 $(2 - \sqrt{3})$ 米 D、 $(2 + \sqrt{3})$ 米

查看试题解析
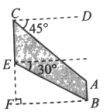4. 如图，某建筑物的顶部有一块宣传牌CD．小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°，沿山坡向上走到B处测得宣传牌顶部C的仰角为45°，已知斜坡AB的坡角为30°， $A B = 10$ 米， $A E = 15$ 米，则宣传牌CD的高度是（）米

A、 $20 - 10 \sqrt{3}$ B、 $20 + 5 \sqrt{3}$ C、 $15 + 5 \sqrt{3}$ D、 $15 \sqrt{3} - 5$

查看试题解析
5. 如图，河坝横断面迎水坡 $A B$ 的坡比为 $1 ： \sqrt{3}$ ，坝高 $B C$ 为4m，则 $A C$ 的长度为（）

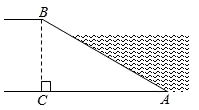A、8m B、 $4 \sqrt{3}$ m C、 $8 \sqrt{3}$ m D、 $\frac{4}{3} \sqrt{3}$ m

查看试题解析
6. 如图，某水库大坝的横断面是梯形 $A B C D$ ，坝高 $D E = 5 m$ ，斜坡 $B C$ 的坡比为 $5 ： 12$ ，则斜坡BC=（）

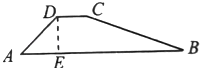A、13m B、8m C、18m D、12m

查看试题解析
7. 如图，港口A在观测站O的正东方向，OA＝4km．某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为（）

A、4km B、2 $\sqrt{3}$ km C、2 $\sqrt{2}$ km D、（ $\sqrt{3}$ ＋1）km

查看试题解析
8. 如图，明明家（图中点O处）门前有一条东西走向的公路，经测得有一水塔（图中点A处）在距她家北偏东60°方向的500米处，那么水塔所在的位置到这条公路的距离是（）

A、 $250 \sqrt{3}$ 米 B、250米 C、 $\frac{500 \sqrt{3}}{3}$ 米 D、 $500 \sqrt{2}$ 米

查看试题解析
9. 东莞市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动，如图，此时无人机在离地面30米的点D处，操控者站在点A处，无人机测得点A的俯角为30°，测得教学楼楼顶点C处的俯角为45°，操控者和教学楼BC的距离为60米，则教学楼BC的高度是（）米．

A、 $60 - 30 \sqrt{3}$ B、 $30 \sqrt{3}$ C、 $30 \sqrt{3} - 30$ D、 $30 \sqrt{3} - 15$

查看试题解析
10. 某水库大坝的横断面是梯形，坝内一斜坡的坡度i＝1∶ $\sqrt{3}$ ，则这个斜坡的坡角为（）

A、30° B、45° C、60° D、90°

查看试题解析

二、填空题

11. 大围山野外滑雪场拥有一定倾斜度的高级道、专业练习道.有一段雪道的垂直高度约为200米，它的坡度为i＝1：3，那么这段雪道长约为米（结果保留根号）.

查看试题解析
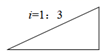12. 如图，轮船在A处观测灯塔C位于北偏西70°方向上，轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行，2小时后到达码头B处，此时，观测灯塔C位于北偏西25°方向上，则灯塔C与码头B的距离是海里.（结果保留根号）

查看试题解析
13. 一条上山直道的坡度为 $1 ： 3$ ，沿这条直道上山，每前进100米所上升的高度为米．

查看试题解析
14. 如图，某无人机兴趣小组在操场上开展活动，此时无人机在离地面 $20 \sqrt{3}$ 米的 $D$ 处，无人机测得操控者 $A$ 的俯角为30°，测得点 $C$ 处的俯角为45°．又经过人工测量操控者 $A$ 和教学楼 $B C$ 之间的水平距离为80米，教学楼 $B C$ 的高度米．（注：点 $A$ 、 $B$ 、 $C$ 、 $D$ 都在同一平面上，参考数据： $\sqrt{3} \approx 1.7$ ，结果保留整数）．

查看试题解析
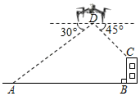15. 如图，测角仪CD竖直放在距建筑物AB底部5m的位置，在D处测得建筑物顶端A的仰角为50°．若测角仪的高度是1.1m，则建筑物AB的高度约为．（结果精确到0.1m，参考数据： $s i n 50 ° \approx 0.77$ ， $c o s 50 ° \approx 0.64$ ， $t a n 50 ° \approx 1.19$ ）

查看试题解析

三、解答题

16. 近几年中学生近视的现象越来越严重，为响应国家的号召，某公司推出了如图1所示的护眼灯，其侧面示意图（台灯底座高度忽略不计）如图2所示，其中灯柱BC＝18cm，灯臂CD＝33cm，灯罩DE＝20cm，BC⊥AB，CD、DE分别可以绕点C、D上下调节一定的角度．经使用发现：当∠DCB＝140°，且ED∥AB时，台灯光线最佳．求此时点D到桌面AB的距离．（精确到0.1cm，参考数值：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）

查看试题解析
17. 如图，某风景区内有一瀑布，AB表示瀑布的垂直高度，在与瀑布底端同一水平位置的点D处测得瀑布顶端A的仰角 $β$ 为45°，斜坡CD的坡度i＝3∶4，CD＝100米，在观景台C处测得瀑布顶端A的仰角 $α$ 为37°，若点B、D、E在同一水平线上，求瀑布的落差AB.（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

查看试题解析
18. 观音湖湿地公园，城市之湖，遂宁之芯，善美之地，是遂宁的一张美丽名片，其中，临仙阁彩拱翼舒，轩敞郎明，格外耀眼.某数学小组为测量临仙阁高度，作出了如下实验：在湖边观景台A处测得临仙阁顶部C的仰角为38°，沿着坡比为1：5的斜坡AB行走 $15 \sqrt{26}$ 后至B处，走到临仙阁塔前广场，此时，发现临仙阁的底部D与广场在同一水平线上，并测得临仙阁顶部C的仰角为63°，求塔高.（结果取整数）
参考数据： $\sin 38^{\circ} \approx 0.62 ， \cos 38^{\circ} \approx 0.79 ， \tan 38^{\circ} \approx 0.78$ ， $\sin 63^{\circ} \approx 0.9 ， \cos 63^{\circ} \approx 0.0.44$ $\tan 63^{\circ} \approx 2$

查看试题解析
19. 如图所示，用测角仪测量远处建筑物的高度AD.已知测角仪的高度为1.6米，在水平线MD上点M处测得建筑物最高点A的仰角为 $22 °$ ，沿MD方向前进24米，达到点N处，测得点A的仰角为 $45 °$ ，求建筑物的高度AD.（结果精确到0.1米，参考数据： $\sin 22 ° \approx 0.37$ ， $\cos 22 ° \approx 0.93$ ， $\tan 22 ° \approx 0.40$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析
20. 如图，某数学兴趣小组为测量一座古塔的高度，在古塔左侧的A点处测得古塔顶端D的仰角为30°，然后向古塔底端C前进30米到达点B处，测得古塔顶端D的仰角为45°，且点A、B、C在同一水平直线上，求古塔CD的高度．

查看试题解析
21. 某校为检测师生体温，在学校门口安装了某型号的测温门，如图为该“测温门”截面示意图，身高1.7米的小聪做了如下实验：当他在地面 $M$ 处时“测温门”开始显示额头温度，此时在额头 $B$ 处测得 $A$ 的仰角为45°；当他在地面 $N$ 处时，“测温门”停止显示额头温度，此时在额头 $C$ 处测得 $A$ 的仰角为58°．如果测温门顶部 $A$ 处距地面的高度 $A D$ 为3.3米，求小聪在有效测温区间 $M N$ 的长度约为多少米？（结果保留一位小数，注：额头到地面的距离以身高计， $s i n 58 ° \approx 0.8$ ， $c o s 58 ° \approx 0.5$ ， $t a n 58 ° \approx 1.6$ ．）

查看试题解析
22. 如图，某飞机于空中 $A$ 处探测到目标 $C$ ，此时飞行高度 $A C = 1200$ m，从飞机上看地平面指挥台 $B$ 的俯角 $α = 37 °$ ．求飞机 $A$ 与指挥台 $B$ 的距离．【参考数据： $s i n 37 ° \approx 0.6$ ， $c o s 37 ° \approx 0.8$ ， $t a n 37 ° \approx 0.75$ 】．

查看试题解析
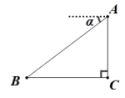23. 如图，一艘快艇A在小岛B的西南方向上相距 $20 \sqrt{2}$ 海里处，另-艘快艇C在快艇A的正东方向上，而小岛B在快艇C的北偏东32°的方向上，已知快艇A的速度是 $40 \sqrt{2}$ 海里/时，若快艇A、C同时出发且同时到达小岛B，求快艇C的速度（精确到个位，参考数据： $s i n 58 ° \approx 0.85$ ， $c o s 58 ° \approx 0.53$ ， $t a n 58 ° \approx 1.6$ ）

查看试题解析
24. 小王是一名经验丰富的户外搜救人员，某日小王接到搜救任务去山里救助一名受伤的户外运动员；来到这座山的东侧A处，为了方便确定受伤人员具体位置，他在A处向上放出一架无人机搜寻，该无人机以每分钟60m的速度沿着仰角为60°的方向上升，5分钟后升到B处，这时小王通过无人机发现受伤人员在他的正西方向，且从无人机上看，受伤人员在它的俯角为45°方向，求小王与受伤人员间AC的距离.（结果保留根号）

查看试题解析

（沪教版）2022-2023学年度第一学期九年级数学25.4 解直角三角形的应用 同步测试

一、单选题

二、填空题

三、解答题

（沪教版）2022-2023学年度第一学期九年级数学25.4 解直角三角形的应用同步测试