(沪教版)2022-2023学年度第一学期九年级数学25.3 解直角三角形 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
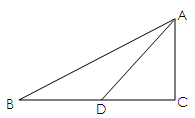
1. 如图是一段索道的示意图. 若 米, , 则洗车从 点到 点上升的高度 的长为( )
 A、 米 B、 米 C、 米 D、 米2. 如图,在中, , , , 则的长为( )
A、 米 B、 米 C、 米 D、 米2. 如图,在中, , , , 则的长为( ) A、 B、2 C、 D、3. 在中, , , 则的值是( )A、 B、 C、 D、4. 如图,已知Rt是斜边边上的高,那么下列结论正确的是( )
A、 B、2 C、 D、3. 在中, , , 则的值是( )A、 B、 C、 D、4. 如图,已知Rt是斜边边上的高,那么下列结论正确的是( )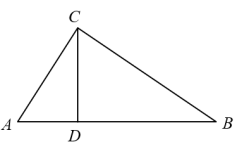 A、 B、 C、 D、5. 在中, , , 那么的长是( )A、 B、 C、 D、6. 某三棱柱的三种视图如图所示,已知俯视图中 , , 下列结论中:①主视图中;②左视图矩形的面积为;③俯视图的正切值为 . 其中正确的个数为( )
A、 B、 C、 D、5. 在中, , , 那么的长是( )A、 B、 C、 D、6. 某三棱柱的三种视图如图所示,已知俯视图中 , , 下列结论中:①主视图中;②左视图矩形的面积为;③俯视图的正切值为 . 其中正确的个数为( ) A、个 B、个 C、个 D、个7. 在 Rt 中, , 如果 , 那么等于( )A、 B、 C、 D、8. 如图,在矩形中, , 点是上一点,将沿直线折叠,点落在矩形的内部点处,若 , 则的长为( )
A、个 B、个 C、个 D、个7. 在 Rt 中, , 如果 , 那么等于( )A、 B、 C、 D、8. 如图,在矩形中, , 点是上一点,将沿直线折叠,点落在矩形的内部点处,若 , 则的长为( ) A、 B、 C、 D、9. 如图,某停车场入口的栏杆从水平位置绕点O旋转到的位置.已知米,若栏杆的旋转角 , 则栏杆端点A上升的垂直距离为( )
A、 B、 C、 D、9. 如图,某停车场入口的栏杆从水平位置绕点O旋转到的位置.已知米,若栏杆的旋转角 , 则栏杆端点A上升的垂直距离为( ) A、米 B、米 C、米 D、米10. 图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形 . 若 , , 则的值为( )
A、米 B、米 C、米 D、米10. 图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形 . 若 , , 则的值为( )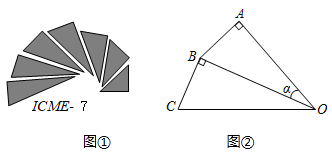 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图是一种手机三脚架,它通过改变锁扣C在主轴 上的位置调节三脚架的高度,其它支架长度固定不变.已知支脚 ,底座 ,且 ,F是 上的固定点,且 .当点B,G,E三点在同一直线上(如图1所示)时,测得 ;若将点C向下移动 ,则点B,G,F三点在同一直线上(如图2),此时点A离地面的高度是 .
 12. 如图,在中, , . 点D、E分别在AB和AC边上, , 把沿着直线DE翻折得 , 如果射线 , 那么 .
12. 如图,在中, , . 点D、E分别在AB和AC边上, , 把沿着直线DE翻折得 , 如果射线 , 那么 .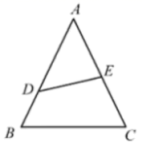 13. 在△ABC中,∠C=90°,如果tan∠A=2,AC=3,那么BC= .14. 如图,在中, , , 点是上一点,点是延长线上一点,已知 , , 则的长为 .
13. 在△ABC中,∠C=90°,如果tan∠A=2,AC=3,那么BC= .14. 如图,在中, , , 点是上一点,点是延长线上一点,已知 , , 则的长为 . 15. 在中, , , , 则 .
15. 在中, , , , 则 .三、解答题
-
16. 如图,在Rt中,∠ACB=90°,CD、CH分别是AB边上的中线和高, , , 求AB、CH的长.
 17. 如图,在△ABC中,∠C = 90°, , D为AC上一点,∠BDC = 45°,CD=6.求AD的长.
17. 如图,在△ABC中,∠C = 90°, , D为AC上一点,∠BDC = 45°,CD=6.求AD的长. 18. 如图,在中, , , , 求BC的长.
18. 如图,在中, , , , 求BC的长.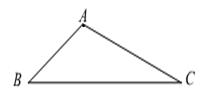 19. 如图,中, , D是的中点,交AC于点E, . 求的正切值.
19. 如图,中, , D是的中点,交AC于点E, . 求的正切值. 20. 如图, 中, , , ,求 的长.
20. 如图, 中, , , ,求 的长.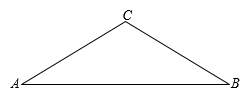 21. 如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.
21. 如图,在Rt△ABC中,∠C=90°,sinB= ,D在BC边上,且∠ADC=45°,AC=5.求∠BAD的正切值.