(沪教版)2022-2023学年度第一学期九年级数学25.2 求锐角的三角比的值 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
1. 在直角ΔABC中,已知∠C=90°, ,求cosA=( )A、 B、 C、 D、2. 将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若 ,则 的值为( )
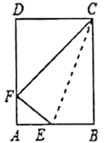 A、 B、 C、 D、3. 在 中, , ,则 的值为( )A、 B、 C、 D、4. 已知 ,则 的度数所属范围是( )A、
A、 B、 C、 D、3. 在 中, , ,则 的值为( )A、 B、 C、 D、4. 已知 ,则 的度数所属范围是( )A、 B、
C、
D、
5. 已知∠A为锐角,且sinA= , 那么∠A等于( )A、15° B、30° C、45° D、60°6. 把Rt△ABC各边的长度都扩大3倍得到Rt△A′B′C′,那么锐角∠A、∠A′的余弦值的关系是( )A、cosA=cosA′ B、cosA=3cosA′ C、3cosA=cosA′ D、不能确定7. 在矩形中,有一个菱形(点、分别在线段、上),记它们的面积分别为和 , 现给出下列命题:①若 , 则 , ②若 , 则.则( ).A、①是真命题,②是真命题 B、①是真命题,②是假命题 C、①是假命题,②是真命题 D、①是假命题,②是假命题8. 已知锐角α满足tan(α+10°)=1, 则锐用α的度数为( )A、20° B、35° C、45° D、50°9. 若数轴上tan30°的值用一个点表示,这个点的位置可能落在段( )
B、
C、
D、
5. 已知∠A为锐角,且sinA= , 那么∠A等于( )A、15° B、30° C、45° D、60°6. 把Rt△ABC各边的长度都扩大3倍得到Rt△A′B′C′,那么锐角∠A、∠A′的余弦值的关系是( )A、cosA=cosA′ B、cosA=3cosA′ C、3cosA=cosA′ D、不能确定7. 在矩形中,有一个菱形(点、分别在线段、上),记它们的面积分别为和 , 现给出下列命题:①若 , 则 , ②若 , 则.则( ).A、①是真命题,②是真命题 B、①是真命题,②是假命题 C、①是假命题,②是真命题 D、①是假命题,②是假命题8. 已知锐角α满足tan(α+10°)=1, 则锐用α的度数为( )A、20° B、35° C、45° D、50°9. 若数轴上tan30°的值用一个点表示,这个点的位置可能落在段( ) A、① B、② C、③ D、④10. 如图坐标系中,O(0,0),A(3,3 ),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE= ,则AC:AD的值是( )
A、① B、② C、③ D、④10. 如图坐标系中,O(0,0),A(3,3 ),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE= ,则AC:AD的值是( ) A、1:2 B、2:3 C、6:7 D、7:8
A、1:2 B、2:3 C、6:7 D、7:8二、填空题
-
11. 计算: .12. 若tanA= , 则∠A= .13. 如图,在 中, , .按以下步骤作图:①分别以点A,B为圆心,以大于 长为半径作弧,两弧交于点E,F;②作直线EF;③以点B为圆心,以BA为半径画弧交直线EF于点G;④连接BG交AC于点P.则 .
 14. 已知 为锐角,且 ,那么 等于.15. 在Rt中, , 如果 , 那么
14. 已知 为锐角,且 ,那么 等于.15. 在Rt中, , 如果 , 那么三、解答题
-
16. 已知是锐角,且 , 计算的值.17. 先化简,再求代数式的值,其中 .18. 已知α是锐角,且sin (α+15°)= ,计算 -4cosα-(π-3.14)0+tanα+ 的值.19. 如图,在 中, , , ,求 的面积.
 20. 某高速公路建设中,需要确定隧道AB的长度.已知在离地面1800m高度C处的飞机上,测量人员测得正前方A , B两点处的俯角分别为60°和45°(即∠DCA=60°,∠DCB=45°).求隧道AB的长.(结果保留根号)
20. 某高速公路建设中,需要确定隧道AB的长度.已知在离地面1800m高度C处的飞机上,测量人员测得正前方A , B两点处的俯角分别为60°和45°(即∠DCA=60°,∠DCB=45°).求隧道AB的长.(结果保留根号) 21. 如图,在△ABC中,∠BAC=90°,AB=AC=2,BD=1,DC=2CE . 求证:cos∠ADE= .
21. 如图,在△ABC中,∠BAC=90°,AB=AC=2,BD=1,DC=2CE . 求证:cos∠ADE= . 22. 如图,边长为1的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF,连接AF,求 的周长.
22. 如图,边长为1的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF,连接AF,求 的周长.
