(沪教版)2022-2023学年度第一学期九年级数学25.1 锐角的三角比的意义 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
1. 在 中, ,则 的值是( ).A、 B、 C、 D、2. 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
 A、 B、 C、 D、3. 如图,在Rt△ABC中,∠C=90°,若AB=5,则BC的长是( )
A、 B、 C、 D、3. 如图,在Rt△ABC中,∠C=90°,若AB=5,则BC的长是( ) A、5sinA B、5cosA C、5tanA D、4. 在中, , , , 则的值为( )A、 B、 C、 D、5. 如图,在△ABC中,∠ACB=90°,AC=BC=8,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=5,则sin∠BFD的值为( )
A、5sinA B、5cosA C、5tanA D、4. 在中, , , , 则的值为( )A、 B、 C、 D、5. 如图,在△ABC中,∠ACB=90°,AC=BC=8,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=5,则sin∠BFD的值为( )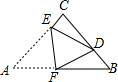 A、 B、 C、 D、6. 在Rt△ABC中,斜边AB的长为m,∠B=40° ,则直角边AC的长是( )A、m sin40° B、mcos40° C、mtan 40° D、7. 如图,在△ABC中,∠C=90°,AB=5,AC=4,则tanB的值是( )
A、 B、 C、 D、6. 在Rt△ABC中,斜边AB的长为m,∠B=40° ,则直角边AC的长是( )A、m sin40° B、mcos40° C、mtan 40° D、7. 如图,在△ABC中,∠C=90°,AB=5,AC=4,则tanB的值是( ) A、 B、 C、 D、8. 如果锐角A的度数是25°,那么下列结论中正确的是( )A、 B、 C、 D、9. 如图,在边长为的小正方形网格中,点都在这些小正方形的顶点上,相交于点 , 则( )
A、 B、 C、 D、8. 如果锐角A的度数是25°,那么下列结论中正确的是( )A、 B、 C、 D、9. 如图,在边长为的小正方形网格中,点都在这些小正方形的顶点上,相交于点 , 则( ) A、 B、 C、 D、210. 中, , 若 , , 下列各式中正确的是A、 B、 C、 D、
A、 B、 C、 D、210. 中, , 若 , , 下列各式中正确的是A、 B、 C、 D、二、填空题
-
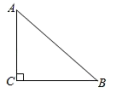
11. 已知在Rt△ABC中,∠C=90°,AC=6,BC=8,则sinB等于 .12. 如图,在中, , , , 则 .
 13. 如图,在正方形网格中,四边形ABCD为菱形,则等于 .
13. 如图,在正方形网格中,四边形ABCD为菱形,则等于 . 14. 在正方形网格中,的位置如图所示,则sin∠BAC的值为 .
14. 在正方形网格中,的位置如图所示,则sin∠BAC的值为 . 15. 如图,在△ABC中,AC=6,BC=8,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是边长为2的正方形,则sin∠FBA= .
15. 如图,在△ABC中,AC=6,BC=8,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是边长为2的正方形,则sin∠FBA= .
三、解答题
-
16. 在 ABC中,AD是BC边上的高,∠C=45°, ,AD=1,求BC的长.
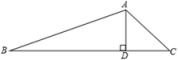 17. 如图,在中, , 延长斜边BC到点D,使 , 联结AD,如果 , 求的值.
17. 如图,在中, , 延长斜边BC到点D,使 , 联结AD,如果 , 求的值. 18. 如图,在RtABC中,∠C=90°,BC=1, , 求tanA与tanB的值.
18. 如图,在RtABC中,∠C=90°,BC=1, , 求tanA与tanB的值.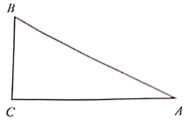 19. 如图,在 中, , , .求 的三个三角函数值.
19. 如图,在 中, , , .求 的三个三角函数值.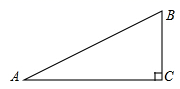 20. 如图,在 中, , , .求: 、 .
20. 如图,在 中, , , .求: 、 . 21. 如图,在 中, 于点D,若 . , ,求 的值.
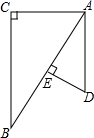
21. 如图,在 中, 于点D,若 . , ,求 的值.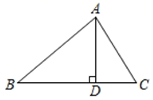 22. 太阳能光伏建筑是太阳能光伏系统与现代绿色环保住宅的完美结合,老刘准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°.求改建后南屋面边沿增加部分AD的长,(结果精确到0.1米)
22. 太阳能光伏建筑是太阳能光伏系统与现代绿色环保住宅的完美结合,老刘准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°.求改建后南屋面边沿增加部分AD的长,(结果精确到0.1米)(参考数据:sin18°≈031,cos18°≈0.95,tan18v≈0.32,sin36°≈0.59)