（沪教版）2022-2023学年度第一学期九年级数学24.7 向量的线性运算同步测试

试卷更新日期：2022-07-16 类型：同步测试

进入出卷网下载

一、单选题

1. 已知 $\vec{m} = 3 \vec{a} - \frac{2}{3} \vec{b}$ ， $\vec{n} = \frac{1}{2} \vec{b} + \frac{1}{4} \vec{a}$ ，那么 $\vec{m} - 4 \vec{n}$ 等于（）

A、 $2 \vec{a} - \frac{8}{3} \vec{b}$ B、 $4 \vec{a} - \frac{4}{3} \vec{b}$ C、 $2 \vec{a} - \frac{4}{3} \vec{b}$ D、 $4 \vec{a} - \frac{8}{3} \vec{b}$

查看试题解析
2. 已知：点C在线段AB上，且AC = 2BC，那么下列等式一定正确的是（）

A、 $\overset{⇀}{A C} + 2 \overset{⇀}{B C} = \frac{4}{3} \overset{⇀}{A B}$ B、 $\overset{⇀}{A C} - 2 \overset{⇀}{B C} = \overset{⇀}{0}$ C、 $| \overset{⇀}{A C} + \overset{⇀}{B C} | = | \overset{⇀}{B C} |$ D、 $| \overset{⇀}{A C} - \overset{⇀}{B C} | = | \overset{⇀}{B C} |$

查看试题解析
3. 在梯形ABCD中，AD∥BC，点E，F分别是边AB，CD的中点，AD= $\frac{1}{2}$ BC， $\vec{B C}$ = $\vec{a}$ ，那么 $\vec{E F}$ 等于（）

A、 $\frac{3}{2} \vec{a}$ B、 $- \frac{3}{2} \vec{a}$ C、 $\frac{3}{4} \vec{a}$ D、 $- \frac{3}{4} \vec{a}$

查看试题解析
4. 如图， $▱ A B C D$ 的对角线AC和BD交于点O ，下列选项中错误的是（）

A、 $\vec{A B} = \vec{D C}$ B、 $\vec{O A} + \vec{O C} = 0$ C、 $| \vec{O B} | = | \vec{O D} |$ D、 $\vec{A C} = 2 \vec{A O}$

查看试题解析
5. 我们规定：若 $\vec{a} = (x_{1} ， y_{1})$ ， $\vec{b} = (x_{2} ， y_{2})$ ，则 $\vec{a} \cdot \vec{b} = x_{1} x_{2} + y_{1} y_{2}$ .例如 $\vec{a} = (1 ， 3)$ ， $\vec{b} = (2 ， 4)$ ，则 $\vec{a} \cdot \vec{b} = 1 \times 2 + 3 \times 4 = 2 + 12 = 14$ .已知 $\vec{a} = (x + 1 ， x - 1)$ ， $\vec{b} = (x - 3 ， 4)$ ，且 $- 2 \leq x \leq 3$ ，则 $\vec{a} \cdot \vec{b}$ 的最小值是（）

A、-6 B、-8 C、-9 D、-7

查看试题解析
6. 点G是 $△ A B C$ 的重心，设 $\vec{A B} = a$ ， $\vec{A C} = b$ ，那么 $\vec{A G}$ 关于 $a$ 和 $b$ 的分解式是（）

A、 $\frac{1}{2} a + \frac{1}{2} b$ B、 $\frac{1}{2} a - \frac{1}{2} b$ C、 $\frac{1}{3} a + \frac{1}{3} b$ D、 $\frac{1}{3} a - \frac{1}{3} b$ ．

查看试题解析
7. 阅读理解：设 $\vec{a} = (x_{1} ， y_{1}) ， \vec{b} = (x_{2} ， y_{2})$ ，若 $\vec{a} ⊥ \vec{b}$ ，则 $\vec{a} \cdot \vec{b} = 0$ ，即 $x_{1} \cdot x_{2} + y_{1} \cdot y_{2} = 0$ ，已知 $\vec{a}$ =(-2，x+1)， $\vec{b}$ =(3，x+2)，且 $\vec{a} ⊥ \vec{b}$ ，则x的值为（）

A、2或-2 B、1或-4 C、-1或4 D、1

查看试题解析
8. 已知在△ABC中，AD是中线，设 $\vec{A B} = \vec{m} ， \vec{A D} = \vec{n}$ ，那么向量 $\vec{B C}$ 用向量 $\vec{m} ， \vec{n}$ 表示为（）

A、 $2 \vec{m} - 2 \vec{n}$ B、 $2 \vec{m} + 2 \vec{n}$ C、 $2 \vec{n} - 2 \vec{m}$ D、 $\vec{n} - \vec{m}$

查看试题解析
9. 已知四边形 $A B C D$ 是矩形，点 $O$ 是对角线 $A C$ 与 $B D$ 的交点.下列四种说法：①向量 $\vec{A O}$ 与向量 $\vec{O C}$ 是相等的向量；②向量 $\vec{O A}$ 与向量 $\vec{O C}$ 是互为相反的向量；③向量 $\vec{A B}$ 与向量 $\vec{C D}$ 是相等的向量；④向量 $\vec{B O}$ 与向量 $\vec{B D}$ 是平行向量．其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 已知：点C在线段AB上，且AC = 2BC，那么下列等式一定正确的是（）

A、 $\vec{A C} + 2 \vec{B C} = \frac{4}{3} \vec{A B}$ B、 $\vec{A C} - 2 \vec{B C} = \vec{0}$ C、 $| \vec{A C} + \vec{B C} | = | \vec{B C} |$ D、 $| \vec{A C} - \vec{B C} | = | \vec{B C} |$

查看试题解析

二、填空题

11. 如图，在平行四边形ABCD中，点M是边CD中点，点N是边BC的中点，设 $A B = \vec{a}$ ， $B C = \vec{b}$ ，那么 $\vec{M N}$ 可用 $\vec{a}$ ， $\vec{b}$ 表示为．

查看试题解析
12. 如图，在 $△ A B C$ 中，中线AD、BE相交于点G，如果 $\vec{A D} = \vec{a} ， \vec{B E} = \vec{b}$ ，那么 $\vec{B C} =$ （用含向量 $\vec{a} ， \vec{b}$ 的式子表示）

查看试题解析
13. 计算： $3 \vec{a} - 2 (\vec{a} - 2 \vec{b})$ = ．

查看试题解析
14. 已知 $a$ 的长度为 $2 ， b$ 的长度为 4 ，且 $b$ 和 $a$ 方向相反，用向量 $a$ 表示向量 $b =$ ．

查看试题解析
15. 已知向量 $\vec{a}$ 、 $\vec{b}$ 、 $\vec{x}$ 满足 $2 (\vec{a} - \vec{x}) = 3 (\vec{b} - \vec{x})$ ，试用向量 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{x}$ ，那么 $\vec{x}$ = ．

查看试题解析

三、解答题

16. 如图，已知：四边形ABCD中，点M、N分别在边BC、CD上， $\frac{C M}{M B} = \frac{C N}{N D} = 2$ ，设 $\vec{A B} = a$ ， $A D = b$ ．
求向量 $\vec{M N}$ 关于 $a$ 、 $b$ 的分解式．

查看试题解析
17. 如图，AD是△ABC中BC边上的中线，点E、F分别是AD、AC的中点，设 $\vec{A C}$ ＝ $\vec{a}$ ， $\vec{A B}$ ＝ $\vec{b}$ ，用 $\vec{a}$ 、 $\vec{b}$ 的线性组合表示向量 $\vec{E F}$ ．

查看试题解析
18. 如图，已知两个不平行的向量 $\vec{a}$ 、 $\vec{b}$ .先化简，再求作： $(\frac{7}{2} \overset{⇀}{a} + \overset{⇀}{b}) - (\frac{3}{2} \overset{⇀}{a} + 2 \overset{⇀}{b})$ .（不要求写作法，但要保留作图痕迹，并指出所作图中表示结论的向量）

查看试题解析
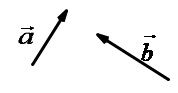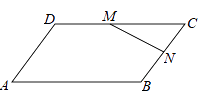19. 如图，已知平行四边形ABCD，点M、N分别是边DC、BC的中点，设 $\overset{⇀}{A B} = \overset{⇀}{a}$ ， $\overset{⇀}{A D} = \overset{⇀}{b}$ ，求向量 $\overset{⇀}{M N}$ 关于 $\overset{⇀}{a}$ 、 $\overset{⇀}{b}$ 的分解式．

查看试题解析
20.
已知：如图，△ABC中，点D是AC边上的一点，且AD：DC=2：1．
=
（1）设 $\vec{B A} = \vec{a} ， \vec{B C} = \vec{b}$ ，先化简，再求作： $(- 2 \vec{a} - \vec{b}) - (- 3 \vec{a} - \frac{3}{2} \vec{b})$ ；
（2）用 $x \vec{a} + y \vec{b}$ （x、y为实数）的形式表示 $\vec{B D}$ ．

查看试题解析

四、综合题

21. 如图，在 $△ A B C$ 中，点F为 $△ A B C$ 的重心，联结AF并延长交BC于点D，联结BF并延长交AC于点E．

(1)、求 $\frac{S_{△ D E F}}{S_{△ A B F}}$ 的值；

(2)、如果 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，用 $\vec{a}$ ， $\vec{b}$ 表示 $\vec{B E}$ 和 $\vec{A F}$ ．

查看试题解析
22. 如图，在平行四边形ABCD中，延长BC到点E，使 $C E = B C$ ，联结AE交DC于点F，设 $\overset{⇀}{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$ ．

(1)、用向量 $\vec{a}$ 、 $\vec{b}$ 表示 $\vec{D E}$ ；

(2)、求作：向量 $\vec{A F}$ 分别在 $\vec{a}$ 、 $\vec{b}$ 方向上的分向量．（不要求写作法，但要写明结论）

查看试题解析
23. 如图，在平行四边形ABCD中，点E在边AD上，CE、BD相交于点F，BF=3DF．

(1)、求AE：ED的值；

(2)、如果 $\vec{D C} = \vec{a}$ ， $\vec{E A} = \vec{b}$ ，试用 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{C F}$ ．

查看试题解析
24. 如图，已知在梯形ABCD中，AB//CD ， AB=12，CD=7，点E在边AD上， $\frac{D E}{A E} = \frac{2}{3}$ ，过点E作EF//AB交边BC于点F.

(1)、求线段EF的长；

(2)、设 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$ ，联结AF ，请用向量 $\vec{a} ， \vec{b}$ 表示向量 $\vec{A F}$ .

查看试题解析

（沪教版）2022-2023学年度第一学期九年级数学24.7 向量的线性运算 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（沪教版）2022-2023学年度第一学期九年级数学24.7 向量的线性运算同步测试