(沪教版)2022-2023学年度第一学期九年级数学24.4 相似三角形的判定 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
1. 如图,D为△ABC中AC边上一点,则添加下列条件不能判定△ABC∽△BDC的是( )
 A、 B、 C、∠ABC=∠BDC D、∠A=∠CBD2. 如图,D是BC上的点,∠ADC=∠BAC,则下列结论正确的是( )
A、 B、 C、∠ABC=∠BDC D、∠A=∠CBD2. 如图,D是BC上的点,∠ADC=∠BAC,则下列结论正确的是( )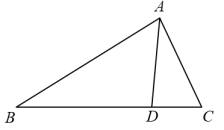 A、△ABC∽△DAB B、△ABC∽△DAC C、△ABD∽△ACD D、以上都对3. 如图,在下列方格纸中的四个三角形,是相似三角形的是( )
A、△ABC∽△DAB B、△ABC∽△DAC C、△ABD∽△ACD D、以上都对3. 如图,在下列方格纸中的四个三角形,是相似三角形的是( )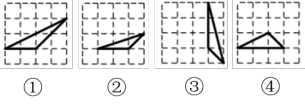 A、①和② B、①和③ C、②和③ D、②和④4. 如图,点P在ΔABC的边AC上,下列条件中不能判定的是( )
A、①和② B、①和③ C、②和③ D、②和④4. 如图,点P在ΔABC的边AC上,下列条件中不能判定的是( ) A、 B、 C、 D、5. 如图,要判定与相似,欲添加一个条件,下列可行的条件有
A、 B、 C、 D、5. 如图,要判定与相似,欲添加一个条件,下列可行的条件有( 1 );(2);(3);(4);(5).
 A、1个 B、2个 C、3个 D、4个6. 如图,下列选项中不能判定△ACD∽△ABC的是( )
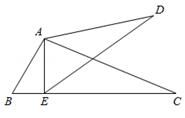
A、1个 B、2个 C、3个 D、4个6. 如图,下列选项中不能判定△ACD∽△ABC的是( ) A、= B、= C、∠ACD=∠B D、∠ADC=∠ACB7. 在中,点在线段上,请添加一个条件使 , 则下列条件中一定正确的是( )A、 B、 C、 D、8. 如图,E是的边的延长线上一点,连接交于F,则图中共有相似三角形( )
A、= B、= C、∠ACD=∠B D、∠ADC=∠ACB7. 在中,点在线段上,请添加一个条件使 , 则下列条件中一定正确的是( )A、 B、 C、 D、8. 如图,E是的边的延长线上一点,连接交于F,则图中共有相似三角形( ) A、4对 B、3对 C、2对 D、1对9. 如图,在 中,点 分别在 边上, 与 不平行,那么下列条件中,不能判定 的是( )
A、4对 B、3对 C、2对 D、1对9. 如图,在 中,点 分别在 边上, 与 不平行,那么下列条件中,不能判定 的是( )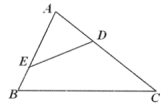 A、 B、 C、 D、10. 如图,AB∥CD,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有( )
A、 B、 C、 D、10. 如图,AB∥CD,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有( ) A、1对 B、2对 C、3对 D、4对
A、1对 B、2对 C、3对 D、4对二、填空题
-
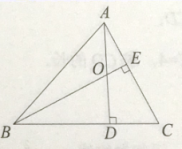
11. 如图,的高AD,BE相交于点O,写出一个与相似的三角形,这个三角形可以是 .
 12. 如图,在中,D是线段上的一点(不与点A,B重合),连接 . 请添加一个条件使与相似,这个条件可以是(写出一个即可).
12. 如图,在中,D是线段上的一点(不与点A,B重合),连接 . 请添加一个条件使与相似,这个条件可以是(写出一个即可). 13. 如图,∠1=∠2,请添加一个条件 , 使△ADE∽△ACB.
13. 如图,∠1=∠2,请添加一个条件 , 使△ADE∽△ACB. 14. 如图,点E在 的边 的延长线上,连接 分别交 、 于F、G.图中相似的两个三角形共有对.
14. 如图,点E在 的边 的延长线上,连接 分别交 、 于F、G.图中相似的两个三角形共有对. 15. 如图,在边长为1的正方形网格中,A、B、C、D、E各点均为格点,则图中能用字母表示 .
15. 如图,在边长为1的正方形网格中,A、B、C、D、E各点均为格点,则图中能用字母表示 .
三、解答题
-
16. 如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.求证:△ADC∽△DEB.
 17. 如图,在平行四边形ABCD中,E为AB边上一点,连接CE,F为CE上一点,且∠DFE=∠A.求证:△DCF∽△CEB.
17. 如图,在平行四边形ABCD中,E为AB边上一点,连接CE,F为CE上一点,且∠DFE=∠A.求证:△DCF∽△CEB. 18. 如图,已知 ,点E、F在线段BD上, , ,求证:
18. 如图,已知 ,点E、F在线段BD上, , ,求证: 19. 在△ABC中,已知点D,E分别是AC,AB边上的中点.
19. 在△ABC中,已知点D,E分别是AC,AB边上的中点.求证:△ADE∽△ACB.