（沪教版）2022-2023学年度第一学期九年级数学24.1 放缩与相似性 同步测试
试卷更新日期：2022-07-16 类型：同步测试
一、单选题
-
1. 下列图形一定相似的是（ ）A、两个平行四边形 B、两个矩形 C、两个正方形 D、两个等腰三角形2. 下列说法正确的是（ ）A、正五边形都相似 B、等腰三角形都相似 C、直角三角形都相似 D、钝角三角形都相似3. 古希腊数学家、天文学家泰勒斯曾在金字塔影子的顶部立一根木杆，借助太阳光线利用数学原理，来测量金字塔的高度．如图，在某一时刻，测得木杆EF的长为2m，它的影长FD为3m，同时测得OA为201 m，求金字塔的高度BO．在解决这个问题的过程中，主要运用的数学知识是（ ）
A、图形的轴对称 B、图形的平移 C、图形的旋转 D、图形的相似4. 在我们日常生活中存在很多较小的或眼睛不易辨清的物体，利用放大镜“放大”，可以使人看得更清楚．如图，利用放大镜可以看清辣椒表面的纹路，这种图形的变换是（ ）
A、平移变换 B、旋转变换 C、轴对称变换 D、相似变换5. 下列命题中， 说法正确的是（ ）A、所有菱形都相似 B、两边对应成比例且有一组角对应相等的两个三角形相似 C、三角形的重心到一个顶点的距离， 等于它到这个顶点对边距离的两倍 D、斜边和直角边对应成比例， 两个直角三角形相似6. 一块矩形绸布的长AB＝a米，宽AD＝1米，按照图中所示的方式将它裁成完全相同的三面矩形彩旗，且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同，那么a的值为（ ）
A、3 B、 C、3 D、7. 下列说法中，正确的是（ ）A、若点M是 上一点，且满足 ，则M是 的黄金分割点 B、所有的菱形都相似 C、所有的矩形都相似 D、所有的等腰三角形都相似8. 在下面的图形中，相似的一组是（ ）A、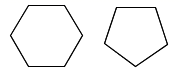
B、
C、
D、
9. 如图，在测量某物体的长度时，若看不清标尺上的刻度，可利用放大镜将标尺上的数码放大，这种图形变换是（ ）
A、平移变换 B、旋转变换 C、轴对称变换 D、相似变换10. 如图，一块矩形ABCD绸布的长AB=a，宽AD=3，按照图中的方式将它裁成相同的三面矩形彩旗，如果裁出的每面彩旗与矩形ABCD绸布相似，则a的值等于（ ）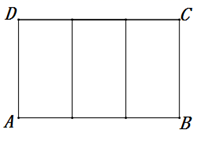
A、 B、 C、 D、二、填空题
-
11. 已知：如图所示，矩形ABCD中，点E、F分别在边AB、CD上，且AEFD是正方形，若矩形BCFE和矩形ABCD相似，且AD=2，则AB的长为 ．
12. 两个相似多边形一组对应边分别为3cm，5cm，那么它们的相似比为 ．13. 下列四个结论：①两个正三角形相似；②两个等腰直角三角形相似；③两个菱形相似；④两个矩形相似；⑤两个正方形相似，其中正确的结论是 ．14. 在一张由复印机通过放大复印出来的纸上，一个面积为2cm2图案的一条边由原来的1cm变成3cm，则这次复印出来的图案的面积是 cm2 ．15. 某课外活动小组的同学在研究某种植物标本（如图所示）时，测得叶片①最大宽度是8cm，最大长度是16cm；叶片②最大宽度是7cm，最大长度是14cm；叶片③最大宽度约为6.5cm，请你用所学数学知识估算叶片③的完整叶片的最大长度，结果约为cm．
三、解答题
-
16. 观察下列图形，指出哪些是相似图形：
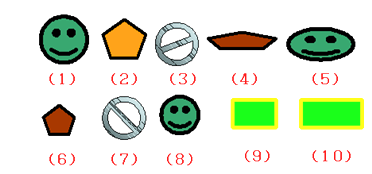17. 如图，G是正方形ABCD对角线AC上一点，作GE⊥AD，GF⊥AB，垂足分别为点E，F．求证：四边形AFGE与四边形ABCD相似．
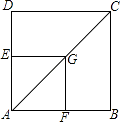18. 图中所示为两幅形状相似的油画A和B，它们的对角线分别长42cm和48cm．问油画A的面积是油画B的百分之几？
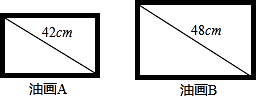19. 如图，四边形ABCD∽四边形EFGH，求∠α、∠β的大小和EH的长度．
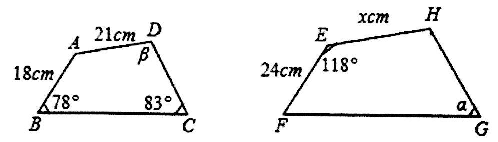20. 在长为10，宽为8的矩形ABCD中，点E在长AD上，F在BC上，若所得到的矩形EFCD∽矩形ABCD，试问AE之长是多少？请说明理由。21.请看下图，并回答下面的问题：
（1）在图（1）中，两个足球的形状相同吗？它们的大小呢？
（2）在图（2）中，两个正方形物体的形状相同吗？
