(沪教版)2022-2023学年度第一学期八年级数学19.10 两点间的距离公式 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
1. 点 离原点的距离是( )A、4 B、7 C、3 D、52. 在平面直角坐标系中,已知定点A(﹣ ,3 )和动点P(a,a),则PA的最小值为( )A、2 B、4 C、2 D、43. 如图,若点 , 点 , 在x轴上找一点P,使最小,则点P坐标为( )
 A、(-5,0) B、(-1,0) C、(0,0) D、(1,0)4. 如图,图中小正方形的组合图形是棱长为1的正方体一种表面展开图,过小正方形的顶点A,B,C,D的线段AB,CD与经过小正方形的顶点E,F的直线交于点M,N,则线段MN的长为( )
A、(-5,0) B、(-1,0) C、(0,0) D、(1,0)4. 如图,图中小正方形的组合图形是棱长为1的正方体一种表面展开图,过小正方形的顶点A,B,C,D的线段AB,CD与经过小正方形的顶点E,F的直线交于点M,N,则线段MN的长为( ) A、2 B、 C、 D、5. 在以O为坐标原点的平面直角坐标系中,点P(-2,1)到坐标原点O的距离为( )A、 B、 C、2 D、56. 古希腊数学家帕普斯利用反比例函数的图象和性质解决了三等分角问题,其方法如下:如图,在直角坐标系中,锐角的边OB在x轴正半轴上,边OA与的图象交于点A,以A为圆心,2OA为半径作圆弧交函数图象于点C,取AC的中点P,则.若 , 则k的值为( )
A、2 B、 C、 D、5. 在以O为坐标原点的平面直角坐标系中,点P(-2,1)到坐标原点O的距离为( )A、 B、 C、2 D、56. 古希腊数学家帕普斯利用反比例函数的图象和性质解决了三等分角问题,其方法如下:如图,在直角坐标系中,锐角的边OB在x轴正半轴上,边OA与的图象交于点A,以A为圆心,2OA为半径作圆弧交函数图象于点C,取AC的中点P,则.若 , 则k的值为( ) A、 B、 C、 D、7. 如图所示,在直角坐标系中, , ,△ABC为等腰直角三角形,以A为位似中心,把△ABC按相似比1:2放大,放大后的图形记作 ,则 的坐标为( )
A、 B、 C、 D、7. 如图所示,在直角坐标系中, , ,△ABC为等腰直角三角形,以A为位似中心,把△ABC按相似比1:2放大,放大后的图形记作 ,则 的坐标为( ) A、 B、 C、 D、8. 如图,在直角坐标系中, , , , 以A为位似中心且在点A同侧,把按相似比放大,放大后的图形记作 , 则的最小值是( )
A、 B、 C、 D、8. 如图,在直角坐标系中, , , , 以A为位似中心且在点A同侧,把按相似比放大,放大后的图形记作 , 则的最小值是( )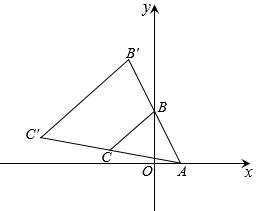 A、 B、 C、 D、39. 抛物线 与 轴的两个交点之间的距离为4,则 的值是( )A、 B、 C、 D、10. 如图, 与 位似,点O是它们的位似中心,其中 ,若点A的坐标为 ,则 的长度为( )
A、 B、 C、 D、39. 抛物线 与 轴的两个交点之间的距离为4,则 的值是( )A、 B、 C、 D、10. 如图, 与 位似,点O是它们的位似中心,其中 ,若点A的坐标为 ,则 的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
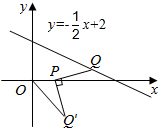
11. 在平面直角坐标系中,Q是直线 上的一个动点,将Q绕点 顺时针旋转 ,得到点 连接 ,则 的最小值为 .
 12. 点P(﹣5,12)到原点的距离是.13. 在直角坐标系内有两点A(-1,1)、B(2,3),若M为x轴上一点,且MA+MB最小,则M的坐标是 , MA+MB=.14. 如图,已知A(0,3),B(2,1),C(2,-3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为 .
12. 点P(﹣5,12)到原点的距离是.13. 在直角坐标系内有两点A(-1,1)、B(2,3),若M为x轴上一点,且MA+MB最小,则M的坐标是 , MA+MB=.14. 如图,已知A(0,3),B(2,1),C(2,-3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为 .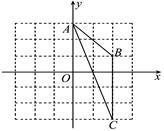 15. 已知直线y=2x﹣2与x轴交于A , 与y轴交于B , 若点C是坐标轴上的一点,且AC=AB , 则点C的坐标为 .
15. 已知直线y=2x﹣2与x轴交于A , 与y轴交于B , 若点C是坐标轴上的一点,且AC=AB , 则点C的坐标为 .三、解答题
-
16. 已知点A(- 3,4),若有一点B(-3,y),使AB=5,求点B的坐标。17. 在平面直角坐标系中,点P(﹣5,2)和点Q(m+1,3m﹣1),当线段PQ与x轴平行时,求线段PQ的长.18. 在平面直角坐标系 中有 四点,其中 , .

(Ⅰ)在下图中描出 四点,再连接 ;
(II)直接写出线段 与线段 的位置关系;
(Ⅲ)若 与 轴交于点 与 轴交于点 ,在线段 上是否存在一点 ,使得三角形 与三角形 的面积相等.若存在,求点 的坐标;若不存在,请说明理由.
19. 如图,已知:关于y的二次函数 的图象与x轴交于点 和点B,与y轴交于点 ,抛物线的对称轴与x轴交于点D. (1)、求二次函数的表达式.(2)、在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.(3)、有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.
(1)、求二次函数的表达式.(2)、在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.(3)、有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.四、综合题
-
20. 设两个点A、B的坐标分别为 , ,则线段AB的长度为: .举例如下:A、B两点的坐标是 , ,则A、B两点之间的距离 .请利用上述知识解决下列问题:(1)、若 , ,且 ,求x的值;(2)、已知△ABC,点A为 、点B为 、点C为 ,求△ABC的面积;(3)、求代数式 的最小值.21. 给出如下定义:在平面直角坐标系 中,已知点 ,这三个点中任意两点间的距离的最小值称为点 的“最短间距”,例如:如图,点 的“最短间距”是1(即 的长).
 (1)、点 的最短间距是;(2)、已知点 ,点 在第三象限.
(1)、点 的最短间距是;(2)、已知点 ,点 在第三象限.①若点O,A,B的最短间距是1,求y的值;
②点O,A,B的“最短间距”的最大值为 ▲ ;
(3)、已知直线l与坐标轴分别交于点 和 ,点 是线段 上的一个动点,当点 的最短间距取到最大值时,则此时点P的坐标.22. 如图,平面直角坐标系中,点O为坐标原点,直线AB分别与x轴、y轴交于点A(4,0),B(0,4).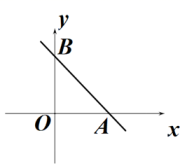 (1)、求直线AB的函数表达式;(2)、若点P为此函数图象上的一点,且AOP是以AO为腰的等腰三角形,求此时P点的坐标.
(1)、求直线AB的函数表达式;(2)、若点P为此函数图象上的一点,且AOP是以AO为腰的等腰三角形,求此时P点的坐标.
