（沪教版）2022-2023学年度第一学期八年级数学19.9 勾股定理 同步测试
试卷更新日期：2022-07-16 类型：同步测试
一、单选题
-
1. 如图，在平面直角坐标系中， ， ，以点A为圆心，AB为半径画弧，交x轴正半轴于点C，点C表示的实数介于（ ）
A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间2. 如图，在Rt△ABC中，∠ACB是直角，点D是AB边上的中点，下列成立的有（ ）①∠A+∠B=90° ②AC2+BC2=AB2 ③2CD=AB ④∠B= 30°
A、①②④ B、①③ C、②④ D、①②③3. 如图，在Rt△ABC中，∠ACB＝90°，AC＝5，BC＝12，将△ABC绕点B顺时针旋转60°，得到△BDE，连接DC交AB于点F，则△ACF与△BDF的周长之和为（ ）
A、44 B、43 C、42 D、414. 下列以a，b，c为边的三角形不是直角三角形的是（ ）A、a＝1，b＝1，c＝ B、a＝2，b＝3，c＝ C、a＝3，b＝5，c＝7 D、a＝6，b＝8，c＝105. 下面图形能够验证勾股定理的有（ ）个
A、4个 B、3个 C、2个 D、1个6. 如图，将直角三角形纸片沿AD折叠，使点B落在AC延长线上的点E处．若AC＝3，BC=4，则图中阴影部分的面积是（ ）
A、 B、 C、 D、7. 为了测量学校的景观池的长AB，在BA的延长线上取一点C，使得米，在点C正上方找一点D（即），测得 ， ， 则景观池的长AB为（ ）
A、5米 B、6米 C、8米 D、10米8. 如图，四边形ABCD中，AB＝3cm，AD＝4cm，BC＝13cm，CD＝12cm，且∠A＝90°，则四边形ABCD的面积为（ ）
A、12cm2 B、18cm2 C、22cm2 D、36cm29. 如图，在网格中，每个小正方形的边长均为1．点A、B，C都在格点上，若BD是ABC的高，则BD的长为（ ）
A、 B、 C、 D、10. 如图，在中， ， AC=4，BC=3，将绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B，D两点间的距离为（ ）
A、 B、 C、3 D、二、填空题
-
11. 在平面直角坐标系中， AOB是等边三角形，点 的坐标为(2，0)，将 AOB绕原点逆时针旋转 ，则点 的坐标为.
12. 如图，等腰△BAC中，∠BAC＝120°，BC＝6，P为射线BA上的动点，M为BC上一动点，则PM+CP的最小值为 ．
13. 如图，△ABC中，AB＝AC＝13，BC＝24，点D在BC上（BD＞CD），△AED与△ACD关于直线AD轴对称，点C的对称点是点E，AE交BC于点F，连结BE，CE.当DE⊥BC时，∠ADE的度数为 ， CE的长为 .
14. 三角形的三边长分别为3，4，5，则最长边上的高为 .15. 如图，在中， ， AB的垂直平分线交AB、AC于点D，E，若 ， ， 则的面积是.
三、解答题
-
16. 《九章算术》中有一道“引葭赴岸”问题：“今有池一丈，葭生其中夹，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何？”题意是：有一个池塘，其底面是边长是10尺的正方形，一根芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B'（如图）．水深和芦苇长各多少尺？
17. 如图，将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起，其中点A′与点A重合，点C′落在边AB上，连接B′C，若∠ACB=∠A′C′B′=90°，AC=BC=6，求B′C的长．
18. 如图，已知四边形ABCD中，AB＝24，BC＝7，CD＝15，AD＝20，∠B＝90°，求四边形的面积.
19. 如图，四边形ABCD中，AB＝3，BC＝4，CD＝12，AD＝13，∠B＝90°，求四边形ABCD的面积.
20. 如图，长方形纸片ABCD ， 沿折痕AE折叠边AD ， 使点D落在BC边上的F处，已知AB＝6，AD＝10，求EC的长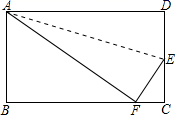
21. 已知，如图， ， ， ，求 的面积.
22. 已知：如图， 中， ， ， ，求 ．
