(沪教版)2022-2023学年度第一学期八年级数学19.8 直角三角形的性质 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
1. 如图,边长为5的等边三角形 中,M是高 所在直线上的一个动点,连接 ,将线段 绕点B逆时针旋转 得到 ,连接 .则在点M运动过程中,线段 长度的最小值是( )
 A、 B、1 C、2 D、2. 如图,△ABC是等边三角形,点E是AC的中点,过点E作EF⊥AB于点F,延长BC交EF的反向延长线于点D,若EF=1,则DF的长为( )
A、 B、1 C、2 D、2. 如图,△ABC是等边三角形,点E是AC的中点,过点E作EF⊥AB于点F,延长BC交EF的反向延长线于点D,若EF=1,则DF的长为( ) A、2 B、2.5 C、3 D、3.53. 已知等边△ABC的边长为12, D是边AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )A、3 B、4 C、8 D、94. 如图,M,A,N是直线l上的三点, , , P是直线l外一点,且 , , 若动点Q从点M出发,向点N移动,移动到点N停止,在APQ形状的变化过程中,依次出现的特殊三角形是( )
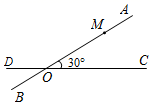
A、2 B、2.5 C、3 D、3.53. 已知等边△ABC的边长为12, D是边AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )A、3 B、4 C、8 D、94. 如图,M,A,N是直线l上的三点, , , P是直线l外一点,且 , , 若动点Q从点M出发,向点N移动,移动到点N停止,在APQ形状的变化过程中,依次出现的特殊三角形是( ) A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形5. 如图,在中, , , 点D为边AB的中点,点P在边AC上,则周长的最小值等于( ).
A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形5. 如图,在中, , , 点D为边AB的中点,点P在边AC上,则周长的最小值等于( ).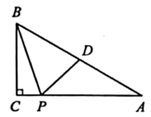 A、 B、 C、 D、6. 如图,为的角平分线, , , 点P,C分别为射线 , 上的动点,则的最小值是( )
A、 B、 C、 D、6. 如图,为的角平分线, , , 点P,C分别为射线 , 上的动点,则的最小值是( ) A、3 B、4 C、5 D、67. 如图所示,在直角三角形ACB中,已知∠ACB=90°,点E是AB的中点,且 , DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( )
A、3 B、4 C、5 D、67. 如图所示,在直角三角形ACB中,已知∠ACB=90°,点E是AB的中点,且 , DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( ) A、5 B、4 C、3 D、28. 如图, 中, , , 平分 ,若 ,则点D到线段 的距离等于( )
A、5 B、4 C、3 D、28. 如图, 中, , , 平分 ,若 ,则点D到线段 的距离等于( ) A、6 B、5 C、8 D、109. 如图,在等腰△ABC中,点M,N都在BC边上,∠BAC=120°,若ME⊥AB于点E,NF⊥AC于点F,点E,F分别为AB,AC的中点,且EM=2.则BC的长为( )
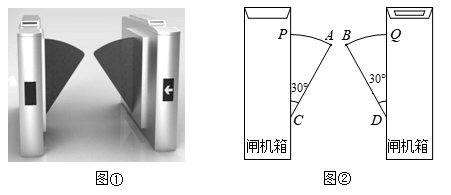
A、6 B、5 C、8 D、109. 如图,在等腰△ABC中,点M,N都在BC边上,∠BAC=120°,若ME⊥AB于点E,NF⊥AC于点F,点E,F分别为AB,AC的中点,且EM=2.则BC的长为( ) A、6 B、8 C、10 D、1210. 如图,Rt△ABC中,∠C=90°,∠B=60°.首先以顶点B为圆心、适当长为半径作弧,在边BC、BA上截取BE、BD;然后分别以点D、E为圆心、以大于 的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若BG=1,P为边AB上一动点,则GP的最小值为( )
A、6 B、8 C、10 D、1210. 如图,Rt△ABC中,∠C=90°,∠B=60°.首先以顶点B为圆心、适当长为半径作弧,在边BC、BA上截取BE、BD;然后分别以点D、E为圆心、以大于 的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若BG=1,P为边AB上一动点,则GP的最小值为( )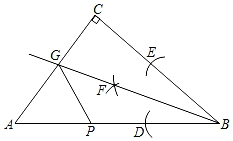 A、无法确定 B、 C、1 D、2
A、无法确定 B、 C、1 D、2二、填空题
-
11. 如图,在三角形纸片 中, ,折叠该纸片,使点C落在 边上的D点处,折痕 与 交于点E,则折痕 的长为.
 12. 若直角三角形斜边上的高和中线长分别是 , ,则它的面积是 .13. 如图,在 中, , ,DE垂直平分AC,交BC于点E, ,则 .
12. 若直角三角形斜边上的高和中线长分别是 , ,则它的面积是 .13. 如图,在 中, , ,DE垂直平分AC,交BC于点E, ,则 . 14. 如图,ABC中, , CD是AB边上的中线,且 , 则AB的长为.
14. 如图,ABC中, , CD是AB边上的中线,且 , 则AB的长为. 15. 如图,某研究性学习小组为测量学校A与河对岸水上乐园B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=1km.据此,可求得学校与水上乐园之间的距离AB等于 km.
15. 如图,某研究性学习小组为测量学校A与河对岸水上乐园B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=1km.据此,可求得学校与水上乐园之间的距离AB等于 km.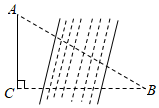
三、解答题
-
16. 如图,在中,∠°,∠°,⊥AB于点D,交AC于点E,如果 , 求的长.
 17. 如图,△ABC中,∠C=90°.
17. 如图,△ABC中,∠C=90°.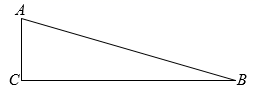 (1)、求作△AEB , 使△AEB是以AB为底的等腰三角形,且使点E在边BC上.(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图形中,若∠CAE:∠EAB=4:1,求∠AEB的度数;(3)、在(2)的条件下,求证:BE=2AC .18. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.
(1)、求作△AEB , 使△AEB是以AB为底的等腰三角形,且使点E在边BC上.(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图形中,若∠CAE:∠EAB=4:1,求∠AEB的度数;(3)、在(2)的条件下,求证:BE=2AC .18. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.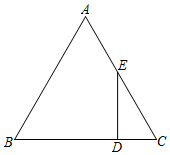 19. 如图,在 中, 于点D , 若 ,求 的长.
19. 如图,在 中, 于点D , 若 ,求 的长. 20. 如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测得到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,你能计算出塔的高度DE吗?写出计算过程.
20. 如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测得到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,你能计算出塔的高度DE吗?写出计算过程. 21. 如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
21. 如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.