(沪教版)2022-2023学年度第一学期八年级数学19.7 直角三角形全等的判定 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
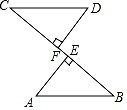
1. 如图, 的外角 的平分线CE与内角 的平分线BE交于点E,若 ,则 的度数为( )
 A、65° B、60° C、55° D、50°2. 如图,在 ABC中,∠ABC的平分线BP与AC的垂直平分线DP相交于点P , 过点P作PF⊥BC于点F , PE⊥AB交BA的延长线于点E . AB=7cm,BC=15cm,则AE的长为( )
A、65° B、60° C、55° D、50°2. 如图,在 ABC中,∠ABC的平分线BP与AC的垂直平分线DP相交于点P , 过点P作PF⊥BC于点F , PE⊥AB交BA的延长线于点E . AB=7cm,BC=15cm,则AE的长为( ) A、3cm B、4cm C、5cm D、6cm3. 如图, , ,垂足分别为D、E,且 ,则直接判定 与 全等的理由是( )
A、3cm B、4cm C、5cm D、6cm3. 如图, , ,垂足分别为D、E,且 ,则直接判定 与 全等的理由是( ) A、SAS B、AAS C、SSS D、HL4. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( )
A、SAS B、AAS C、SSS D、HL4. 如图,点E是的中点, , , 平分 , 下列结论:①;②;③;④.其中正确的是( ) A、①②④ B、①②③④ C、②③④ D、①③5. 如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A、①②④ B、①②③④ C、②③④ D、①③5. 如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( ) A、40° B、60° C、45° D、50°6. 如图,AC⊥BE于点C,DF⊥BE于点F,BC=EF,如果添加一个条件后,可以直接利用“HL”来证明△ABC≌△DEF,则这个条件应该是( )
A、40° B、60° C、45° D、50°6. 如图,AC⊥BE于点C,DF⊥BE于点F,BC=EF,如果添加一个条件后,可以直接利用“HL”来证明△ABC≌△DEF,则这个条件应该是( ) A、AC=DE B、∠D=∠A C、AB=DE D、∠B=∠E7. 如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )个
A、AC=DE B、∠D=∠A C、AB=DE D、∠B=∠E7. 如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )个 A、1 B、2 C、3 D、48. 如图,在 和 中, , , ,过A作 ,垂足为F, 交 的延长线于点G,连接 .若四边形 的面积为12, ,则 的长是( )
A、1 B、2 C、3 D、48. 如图,在 和 中, , , ,过A作 ,垂足为F, 交 的延长线于点G,连接 .若四边形 的面积为12, ,则 的长是( ) A、2 B、2.5 C、3 D、9. 如下图,要用“HL”判断Rt△ABC和Rt△DEF全等的条件是( )
A、2 B、2.5 C、3 D、9. 如下图,要用“HL”判断Rt△ABC和Rt△DEF全等的条件是( ) A、AC=DF,BC=EF B、∠A=∠D,AB=DE C、AC=DF,AB=DE D、∠B=∠E,BC=EF10. 如图,∠A=∠D=90°,AC=DB,则 ABC≌ DCB的依据是( )
A、AC=DF,BC=EF B、∠A=∠D,AB=DE C、AC=DF,AB=DE D、∠B=∠E,BC=EF10. 如图,∠A=∠D=90°,AC=DB,则 ABC≌ DCB的依据是( ) A、HL B、ASA C、AAS D、SAS
A、HL B、ASA C、AAS D、SAS二、填空题
-
11. 如图,∠C=∠D=90°,AC=AD,请写出一个正确的结论 .
 12. 如图, , , ,则 .
12. 如图, , , ,则 . 13. 如图所示,△ABC中∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=13cm,则△DBE的周长为.
13. 如图所示,△ABC中∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=13cm,则△DBE的周长为. 14. 如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=4,则BE=.
14. 如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=4,则BE=. 15. 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是.(写一种即可)
15. 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是.(写一种即可)
三、解答题
-
16. 如图所示,在 中, ,AD平分 交BC于D, 于E,求证 的周长等于AB的长
 17. 已知:如图,∠B=∠C=90°, AF=DE , BE=CF . 求证:AB=DC .
17. 已知:如图,∠B=∠C=90°, AF=DE , BE=CF . 求证:AB=DC . 18. 如图所示,点B , E , C , F在同一条直线上,能否由 , 来证明AC∥DE?如果能,请给出证明;如果不能,请从下列四个条件中再选择一个合适的条件,使AC∥DE成立,并说明理由.供选择的四个条件:① ;② ;③AB∥DF;④ .
18. 如图所示,点B , E , C , F在同一条直线上,能否由 , 来证明AC∥DE?如果能,请给出证明;如果不能,请从下列四个条件中再选择一个合适的条件,使AC∥DE成立,并说明理由.供选择的四个条件:① ;② ;③AB∥DF;④ . 19. 如图,点E、F在BC上,BE=FC , AB=DC , ∠A=∠D=90°.求证:∠B=∠C .
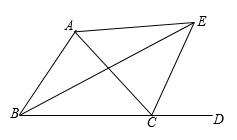
19. 如图,点E、F在BC上,BE=FC , AB=DC , ∠A=∠D=90°.求证:∠B=∠C . 20. 如图,在△ABC中,AC=BC,直线l经过点C,过A、B两点分别作直线l的垂线AE、BF,垂足分别为E、F,AE=CF,求证:∠ACB=90°
20. 如图,在△ABC中,AC=BC,直线l经过点C,过A、B两点分别作直线l的垂线AE、BF,垂足分别为E、F,AE=CF,求证:∠ACB=90°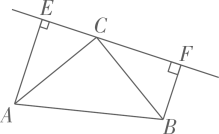 21. 如图,在三角形ABC中,∠C=90°,DE⊥AB于点D,DB=BC,求证:AC=AE+DE.
21. 如图,在三角形ABC中,∠C=90°,DE⊥AB于点D,DB=BC,求证:AC=AE+DE.