(沪教版)2022-2023学年度第一学期八年级数学19.5 角的平分线 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
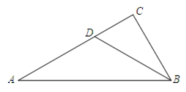
1. 如图,CD是等腰三角形 △ABC底边上的中线,BE平分∠ABC,交CD于点E,AC=8,DE=2,则 △ BCE的面积是( )
 A、4 B、6 C、8 D、122. 如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( )
A、4 B、6 C、8 D、122. 如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( ) A、在∠B的平分线与DE的交点处 B、在线段AB、AC的垂直平分线的交点处 C、在∠B的平分线与DE的垂直平分线的交点处 D、在∠A的平分线与DE的垂直平分线的交点处3. 下列语句中是命题的有( )
A、在∠B的平分线与DE的交点处 B、在线段AB、AC的垂直平分线的交点处 C、在∠B的平分线与DE的垂直平分线的交点处 D、在∠A的平分线与DE的垂直平分线的交点处3. 下列语句中是命题的有( )①线段垂直平分线上的点到线段两端的距离相等;②作点A关于直线l的对称点A'; ③三边对应相等的两个三角形全等吗?④角平分线上的点到角两边的距离相等.
A、1个 B、2个 C、3个 D、4个4. 如图,P是平分线上一点,OP=10, , 在绕点P旋转的过程中始终保持不变,其两边和OA,OB分别相交于M,N,下列结论:①是等边三角形;②MN的值不变;③OM+ON=10;④四边形PMON面积不变.其中正确结论的个数为( ) A、4 B、3 C、2 D、15. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP,并廷长交BC于点D,则下列说法中正确的个数是( )
A、4 B、3 C、2 D、15. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP,并廷长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④若AD=2dm,则点D到AB的距离是1dm
⑤S△DAC:S△DAB=1:2
 A、2 B、3 C、4 D、56. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A、2 B、3 C、4 D、56. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( ) A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:57. 如图,在中, , 是的平分线, , 垂足是E.若 , , 则的长为( )
A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:57. 如图,在中, , 是的平分线, , 垂足是E.若 , , 则的长为( ) A、4 B、3 C、2 D、18. 在△ABC中,AD是角平分线,点E、F分别是线段AC、CD的中点,若△ABD、△EFC的面积分别为21、7,则的值为( )
A、4 B、3 C、2 D、18. 在△ABC中,AD是角平分线,点E、F分别是线段AC、CD的中点,若△ABD、△EFC的面积分别为21、7,则的值为( ) A、 B、 C、 D、9. 如图,是△的角平分线,于 , 点分别是上的点, , △与△的面积分别是和 , 则△的面积是( )
A、 B、 C、 D、9. 如图,是△的角平分线,于 , 点分别是上的点, , △与△的面积分别是和 , 则△的面积是( ) A、a-b B、 C、 D、10. 如图,在△ABC中,∠B=90°,∠A=30°,作AC的垂直平分线交AB于点D,交AC于点E,若DE=3,则BD的长度是( )
A、a-b B、 C、 D、10. 如图,在△ABC中,∠B=90°,∠A=30°,作AC的垂直平分线交AB于点D,交AC于点E,若DE=3,则BD的长度是( ) A、3 B、2 C、 D、
A、3 B、2 C、 D、二、填空题
-
11. 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,AD=4,CD=2,那么∠A=度.
 12. 如图所示,已知∠AOB=40°,现按照以下步骤作图:①在OA,OB上分别截取线段OD,OE,使OD=OE;②分别以D,E为圆心,以DE长为半径画弧,在∠AOB内两弧交于点C;③作射线OC;④连接DC、EC.则∠OEC的度数为 .
12. 如图所示,已知∠AOB=40°,现按照以下步骤作图:①在OA,OB上分别截取线段OD,OE,使OD=OE;②分别以D,E为圆心,以DE长为半径画弧,在∠AOB内两弧交于点C;③作射线OC;④连接DC、EC.则∠OEC的度数为 . 13. 如图,中, , , 是的平分线,于点 , 已知 , 则cm.
13. 如图,中, , , 是的平分线,于点 , 已知 , 则cm. 14. 如图,四边形 中, ,连接 , 平分 ,E是直线 上一点, , ,则 的长为 .
14. 如图,四边形 中, ,连接 , 平分 ,E是直线 上一点, , ,则 的长为 .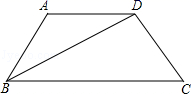 15. 如图, 是 的平分线, 于点 , 于点 , , , 的面积是36,则 的长是 .
15. 如图, 是 的平分线, 于点 , 于点 , , , 的面积是36,则 的长是 .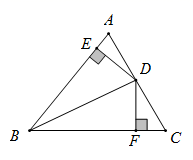
三、解答题
-
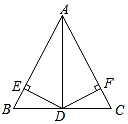
16. 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,求证:BE=CF.
 17. 如图,在△ABC中,∠C = 90°,AD是∠BAC的平分线,过点D作DE⊥AB. DE恰好是AB的垂直平分线.CD与DB有怎样的数量关系?请说明理由.
17. 如图,在△ABC中,∠C = 90°,AD是∠BAC的平分线,过点D作DE⊥AB. DE恰好是AB的垂直平分线.CD与DB有怎样的数量关系?请说明理由. 18. 已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.
18. 已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.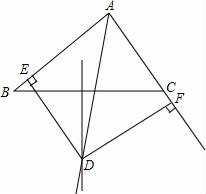 19. 已知:如图, 为 的角平分线,且 , 为 延长线上的一点, ,过 作 , 为垂足.求证:
19. 已知:如图, 为 的角平分线,且 , 为 延长线上的一点, ,过 作 , 为垂足.求证:① ;
② ;
③ .
 20. 太和中学校园内有一块直角三角形(Rt ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在 ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.
20. 太和中学校园内有一块直角三角形(Rt ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在 ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积. 21. 已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF.
21. 已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF.


