（沪教版）2022-2023学年度第一学期八年级数学19.3 逆命题和逆定理 同步测试

试卷更新日期：2022-07-16 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 下列命题中，其逆命题是真命题的命题个数有（    ）

    ⑴全等三角形的对应边相等； ⑵对顶角相等；

    ⑶等角对等边；             ⑷全等三角形的面积相等．

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 2. 下列命题中，逆命题错误的是（   ）
    A、两直线平行，同旁内角互补 B、对顶角相等 C、直角三角形的两个锐角互余 D、直角三角形两条直角边的平方和等于斜边的平方

    查看试题解析

  • 3. 以下命题的逆命题为真命题的是（    ）
    A、邻补角相等 B、同旁内角互补，两直线平行 C、若 a=b ，则 a2=b2 D、若 a>0 ， b>0 ，则 a2+b2>0

    查看试题解析

  • 4. “对顶角相等”的逆命题是（   ）
    A、如果两个角是对顶角，那么这两个角相等   B、如果两个角相等，那么这两个角是对顶角   C、如果两个角不是对顶角，那么这两个角不相等   D、如果两个角不相等，那么这两个角不是对顶角

    查看试题解析

  • 5. 对于下列命题：①若a2＞b2 ， 则|a|＞|b|；②若a+b＝0，则|a|＝|b|；③等边三角形的三个内角都相等；其中原命题与逆命题均为真命题的是（   ）
    A、①②③ B、①② C、①③ D、②③

    查看试题解析

  • 6. 下列命题的逆命题是假命题的是（    ）
    A、直角三角形的两个锐角互余 B、有两边相等的三角形是等腰三角形 C、相等的两个角是对顶角 D、如果a＞0，b＞0，那么a+b＞0

    查看试题解析

  • 7. 下列语句正确的有（   ）个.

    ①“对顶角相等”的逆命题是真命题.

    ②“同角（或等角）的补角相等”是假命题.

    ③立方根等于它本身的数是非负数.

    ④用反证法证明：如果在 △ABC 中， ∠C=90° ，那么 ∠A 、 ∠B 中至少有一个角不大于45°时，应假设 ∠A>45° ， ∠B>45° .

    ⑤如果一个等腰三角形的两边长分别是 2cm 和 5cm ，则周长是 9cm 或 12cm .

    A、4 B、3 C、2 D、1

    查看试题解析

  • 8. 下列命题的逆命题是假命题的是（  ）
    A、直角三角形两锐角互余 B、全等三角形对应角相等 C、两直线平行，同位角相等 D、角平分线上的点到角两边的距离相等

    查看试题解析

  • 9. 下列命题中，其逆命题是假命题的是（ ）
    A、等腰三角形的两个底角相等 B、若两个数的差为正数，则这两个数都为正数 C、若ab＝1，则a与b互为倒数 D、如果|a|＝|b|，那么a2＝b2

    查看试题解析

  • 10. 下列命题的逆命题不正确的是（  ）
    A、两直线平行，内错角相等 B、直角三角形中斜边上的中线等于斜边的一半 C、对顶角相等 D、等腰三角形的两个底角相等

    查看试题解析

二、填空题

  • 11. “全等三角形的对应边相等”的逆命题是： ．

    查看试题解析

  • 12. 命题“如果ab＝0，那么a+b＝0”的逆命题为 ．

    查看试题解析

  • 13. 把命题：“内错角相等”改写成“如果…那么…”的形式是；该命题是命题（填“真”或“假”）.

    查看试题解析

  • 14. 已知命题：“如果两个三角形全等，那么这两个三角形的面积相等.”写出它的逆命题： ， 该逆命题是命题（填“真”或“假”）.

    查看试题解析

  • 15. “等腰三角形底边上的高线与中线互相重合”的逆命题是 ． 这个逆命题是命题．（真、假）

    查看试题解析

三、解答题

  • 16. 写出命题：“等腰三角形两腰上的高相等”的逆命题，并证明其逆命题是真命题.（要求写出已知、求证和证明过程）

    .

    查看试题解析

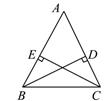  • 17. 写出命题“等腰三角形两腰上的高线长相等”的逆命题，判断这个命题的真假，并说明理由．

    查看试题解析

  • 18. 写出命题“等腰三角形底边上的高线与顶角平分线重合”的逆命题，这个逆命题是真命题吗？请证明你的结论

    查看试题解析

  • 19. 按要求完成下列各小题．

    （1）请写出以下命题的逆命题：

    ①相等的角是内错角；

    ②如果a+b＞0，那么ab＞0；

    （2）判断（1）中①的原命题和逆命题是否为逆定理．

    查看试题解析

  • 20. 写出以下命题的逆命题，判断逆命题的真假．若为假命题，请举反例；若为真命题，请给予证明．

    （1）一次函数y=kx+b，若k＞0，b＜0，则它的图象不经过第二象限；

    （2）等腰三角形底边上的中点到两腰的距离相等．

    查看试题解析

  • 21. 写出命题“如果一个三角形是直角三角形，那么它的两个锐角的角平分线所夹的锐角是45°”的逆命题，并证明这个命题是真命题．

    查看试题解析

  • 22. 写出命题“有两角互余的三角形是直角三角形”的逆命题并证明．

    查看试题解析

  • 23. 写出下列各命题的逆命题，并判断原命题和逆命题是不是互逆定理．

    （1）相等的角是内错角；

    （2）角平分线上的点到角的两边的距离相等．

    查看试题解析

  • 24. （1）写出命题“全等三角形的面积相等”的逆命题，并判断真假；

    （2）若该命题的逆命题为真命题，请证明；若该命题的逆命题为假命题，请举出反例．

    查看试题解析