(沪教版)2022-2023学年度第一学期八年级数学18.3 反比例函数 同步测试
试卷更新日期:2022-07-16 类型:同步测试
一、单选题
-
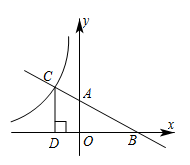
1. 如图所示,在平面直角坐标系xOy中,点A、B、C为反比例函数y=(k>0)上不同的三点,连接OA、OB、OC,过点A作AD⊥y轴于点D,过点B、C分别作BE,CF垂直x轴于点E、F,OC与BE相交于点M,记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3 , 则( )
 A、S1=S2+S3 B、S2=S3 C、S3>S2>S1 D、S1S2<S322. 如果正比例函数图象与反比例函数图象的一个交点的坐标为(3,-4),那么另一个交点的坐标为( )A、(-3,-4) B、(3,4) C、(−3,4) D、(-4,3)3. 在反比例函数y=的图像上有三点A1(x1 , y1)、A2(x2 , y2)、A3(x3 , y3),已知x1< x2<0<x3则下列各式中,正确的是( )A、y1<y2<y3 B、y3< y2< y1 C、y2< y1< y3 D、y3< y1< y24. 已知函数中,在每个象限内,的值随的值增大而增大,那么它和函数在同一直角坐标平面内的大致图像是( ).A、
A、S1=S2+S3 B、S2=S3 C、S3>S2>S1 D、S1S2<S322. 如果正比例函数图象与反比例函数图象的一个交点的坐标为(3,-4),那么另一个交点的坐标为( )A、(-3,-4) B、(3,4) C、(−3,4) D、(-4,3)3. 在反比例函数y=的图像上有三点A1(x1 , y1)、A2(x2 , y2)、A3(x3 , y3),已知x1< x2<0<x3则下列各式中,正确的是( )A、y1<y2<y3 B、y3< y2< y1 C、y2< y1< y3 D、y3< y1< y24. 已知函数中,在每个象限内,的值随的值增大而增大,那么它和函数在同一直角坐标平面内的大致图像是( ).A、 B、
B、 C、
C、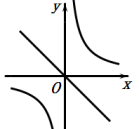 D、
D、 5. 下列函数中,函数值y随x的增大而增大的是( )A、 ; B、 ; C、 ; D、 .6. 已知三点 、 和 都在反比例函数 的图像上,若 ,则m、n和t的大小关系是( )A、 B、 C、 D、7. 如图,A、C是函数 的图象上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D.记 的面积为 , 的面积为 ,则 和 的大小关系是( )
5. 下列函数中,函数值y随x的增大而增大的是( )A、 ; B、 ; C、 ; D、 .6. 已知三点 、 和 都在反比例函数 的图像上,若 ,则m、n和t的大小关系是( )A、 B、 C、 D、7. 如图,A、C是函数 的图象上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D.记 的面积为 , 的面积为 ,则 和 的大小关系是( ) A、 B、 C、 D、由A、C两点的位置确定8. 已知正比例函 (k是常数, )中y随x的増大而增大,那么它和函数 (k是常数,k≠0)在同一平面直角坐标系内的大致图像可能是( )A、
A、 B、 C、 D、由A、C两点的位置确定8. 已知正比例函 (k是常数, )中y随x的増大而增大,那么它和函数 (k是常数,k≠0)在同一平面直角坐标系内的大致图像可能是( )A、 B、
B、 C、
C、 D、
D、 9. 反比例函数 的图象如图所示,以下结论:
9. 反比例函数 的图象如图所示,以下结论: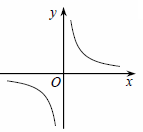
① 常数m <-1;
② 在每个象限内,y随x的增大而增大;
③ 若A(-1,h),B(2,k)在图象上,则h<k;
④ 若P(x,y)在图象上,则P′(-x,-y)也在图象上.
其中正确的是( )
A、①② B、②③ C、③④ D、①④10. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )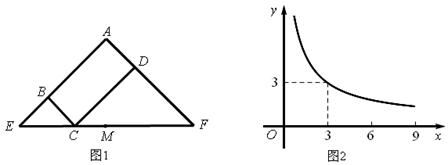 A、当x=3时,EC<EM B、当y=9时,EC>EM C、当x增大时,EC·CF的值增大。 D、当y增大时,BE·DF的值不变。
A、当x=3时,EC<EM B、当y=9时,EC>EM C、当x增大时,EC·CF的值增大。 D、当y增大时,BE·DF的值不变。二、填空题
-
11. 若、两点都在函数的图像上,且< , 则k的取值范围是 .12. 已知反比例函数的图象位于第二、四象限,则k的取值范围是 .13. 在平面直角坐标系中,点A(﹣4,1)为直线y=kx(k≠0)和双曲线y= (m≠0)的一个交点,点B(﹣5,0),如果在直线y=kx上有一点P , 使得S△ABP=2S△ABO , 那么点P的坐标是 .14. 如果反比例函数y= 的图象位于第二、四象限,那么满足条件的正整数k的值是.15. 如图,正比例函数y=﹣2x与一次函数y=ax+b的图象交于点P(﹣1,m),那么二元一次方程组 的解为 .
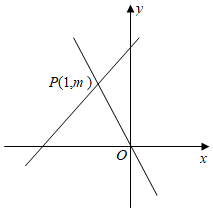
三、解答题
-
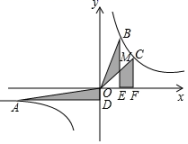
16. 已知反比例函数y=(k≠0)的图象与一次函数y= mx+ n(k≠0)的图象相交于A(a,-1),B(-1,3)两点,求反比例函数和一次函数的解析式.17. 如图,在平面直角坐标系中,四边形OABC为矩形,点D为AB的中点.一次函数y=﹣3x+6的图象经过点C、D,反比例函数y=(x>0),求k的值.
 18. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
18. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
Ⅰ 试确定上述反比例函数和一次函数的表达式;
Ⅱ 连OB,在x轴上取点C,使 ,并求 的面积;
Ⅲ 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
19. 设 为非零实数,两个函数 与 的图象相交于 , 两点,若 ,求 的值.20. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点 , 与y轴交于点C,与反比例的图象交于点A.点B为AC的中点.求一次函数和反比例的解析式.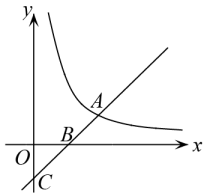 21. 已知一次函数 和反比例函数 .当 时,两个函数自变量的值相等,求反比例函数的表达式.
21. 已知一次函数 和反比例函数 .当 时,两个函数自变量的值相等,求反比例函数的表达式.