(沪教版)2022-2023学年度第一学期七年级数学11.6 轴对称 同步测试
试卷更新日期:2022-07-15 类型:同步测试
一、单选题
-
1. 在中, , , 将折叠,使点A落在点B处,折痕为 , 连结 , 则的周长为( )
 A、20 B、16 C、10 D、82. 平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、3. 如图,四边形ABCD为一长方形纸带,AD∥BC,将四边形ABCD沿EF折叠,C、D两点分别与C′、D′对应,若∠1=2∠2,则∠3的度数为( )
A、20 B、16 C、10 D、82. 平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、3. 如图,四边形ABCD为一长方形纸带,AD∥BC,将四边形ABCD沿EF折叠,C、D两点分别与C′、D′对应,若∠1=2∠2,则∠3的度数为( ) A、50° B、54° C、58° D、62°4. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、5. 如图,在矩形中, , , 动点满足 , 则点到、两点距离之和的最小值为( )
A、50° B、54° C、58° D、62°4. 在平面直角坐标系中,点关于x轴对称的点的坐标是( )A、 B、 C、 D、5. 如图,在矩形中, , , 动点满足 , 则点到、两点距离之和的最小值为( ) A、 B、 C、 D、6. 如图,在中, , , 以点C为圆心,适当的长为半径作弧,分别交AC,BC于点E,F;分别以点E,F为圆心,大于的长为半径作弧,两弧交于点D;作射线CD.若点M为边BC上一动点,点N为射线CD上一动点,则的最小值为( )
A、 B、 C、 D、6. 如图,在中, , , 以点C为圆心,适当的长为半径作弧,分别交AC,BC于点E,F;分别以点E,F为圆心,大于的长为半径作弧,两弧交于点D;作射线CD.若点M为边BC上一动点,点N为射线CD上一动点,则的最小值为( )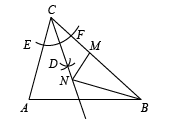 A、3 B、 C、4 D、7. 如图,已知A(3,1)与B(1,0),PQ是直线上的一条动线段且(Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( )
A、3 B、 C、4 D、7. 如图,已知A(3,1)与B(1,0),PQ是直线上的一条动线段且(Q在P的下方),当AP+PQ+QB最小时,Q点坐标为( ) A、( , ) B、( , ) C、(0,0) D、(1,1)8. 如图,将△ABD沿△ABC的角平分线AD所在直线翻折,点B在AC边上的落点记为点E.已知∠C=20°、AB+BD=AC,那么∠B等于( )
A、( , ) B、( , ) C、(0,0) D、(1,1)8. 如图,将△ABD沿△ABC的角平分线AD所在直线翻折,点B在AC边上的落点记为点E.已知∠C=20°、AB+BD=AC,那么∠B等于( ) A、80° B、60° C、40° D、30°9. 已知点与点关于轴对称,则( )A、1 B、-1 C、-2021 D、202210. 如图,∠MON=40°,以O为圆心,4为半径作弧交OM于点A,交ON于点B,分别以点A,B为圆心,大于的长为半径画弧,两弧在∠MON的内部相交于点C,画射线OC交于点D,E为OA上一动点,连接BE,DE,则阴影部分周长的最小值为( )
A、80° B、60° C、40° D、30°9. 已知点与点关于轴对称,则( )A、1 B、-1 C、-2021 D、202210. 如图,∠MON=40°,以O为圆心,4为半径作弧交OM于点A,交ON于点B,分别以点A,B为圆心,大于的长为半径画弧,两弧在∠MON的内部相交于点C,画射线OC交于点D,E为OA上一动点,连接BE,DE,则阴影部分周长的最小值为( )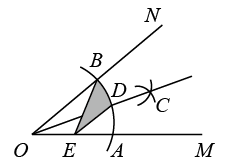 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 点 关于y轴的对称点的坐标是.12. 将图1长方形纸带沿EF折叠成图2,已知∠DEF=20°,则∠BGD的度数等于.
 13. 把一张长方形纸片沿折叠后,与的交点为 , 、分别在、的位置上,若 , 则.
13. 把一张长方形纸片沿折叠后,与的交点为 , 、分别在、的位置上,若 , 则. 14. 如图,把一张长方形纸片ABCD折叠,使得点D落在边BC上的点处,已知∠1=20°,则∠2=° .
14. 如图,把一张长方形纸片ABCD折叠,使得点D落在边BC上的点处,已知∠1=20°,则∠2=° . 15. 如图,∠AOB=30°,点M,N分别在边0A,OB上,且OM=1,ON=3,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值是
15. 如图,∠AOB=30°,点M,N分别在边0A,OB上,且OM=1,ON=3,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值是
三、解答题
-
16. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
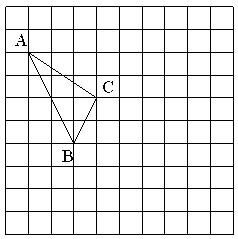
( 1 )请在如图所示的网格平面内作出平面直角坐标系;
( 2 )请作出△ABC关于y轴对称的△A′B′C′;
( 3 )写出点B′的坐标.
17. 在下图给出一个图案的左半部分,其中虚线是这个图案的对称轴.请你画出这个图案的右半部分,使它组成一个完整的图案.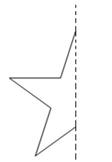 18. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,点B的坐标为 .
18. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,点B的坐标为 .
( 1 )作出 关于x轴对称的 ,并写出点 的坐标;
( 2 )作出 关于y轴对称的 ,并写出点 的坐标,
19. 如图,将一张长方形纸片按如图方式折叠,猜想折痕EF,EG的位置关系,并说明理由.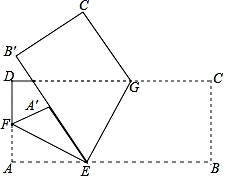 20. 如图所示,在直角坐标系下,图1中的图案“A"经过变换分别变成图2至图3中的相应图案(虚线对应于图1中的图案),试写出图2至图3中各顶点的坐标,探索每次变换前后图案发生了什么变化,对应点的坐标之间有什么关系?
20. 如图所示,在直角坐标系下,图1中的图案“A"经过变换分别变成图2至图3中的相应图案(虚线对应于图1中的图案),试写出图2至图3中各顶点的坐标,探索每次变换前后图案发生了什么变化,对应点的坐标之间有什么关系? 21. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 .
21. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 .
⑴请画出 关于x轴对称的 ,并写出点 的坐标;
⑵以O为对称中心,画出 关于O成中心对称的图形 ;
⑶请用无刻度的直尺画出 的平分线 (点Q在线段 上)(保留作图辅助线).
22. 如图所示,在平面直角坐标系中△ABC的三个顶点坐标分别为A(﹣2,4),B(-4,2),C(﹣3,1).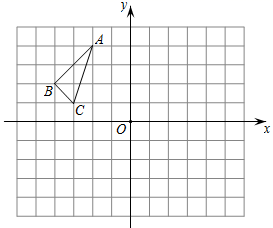
(1)作出△ABC关于x轴对称的△A1B1C1 , 并直接写出A1点的坐标
(2)作出△ABC关于y轴对称的△A2B2C2 , 并直接写出B2点的坐标
(3)在(1)(2)的条件下,若点P在x轴上,当A1P+B2P的值最小时,直接写出A1P+B2P的最小值