(沪教版)2022-2023学年度第一学期七年级数学11.3 旋转对称图形与中心对称图形 同步测试
试卷更新日期:2022-07-15 类型:同步测试
一、单选题
-
1. 下列图形中,不是旋转对称图形的是( )A、正三角形 B、等腰梯形 C、正五边形 D、正六边形2. 如图,是一个纸折的小风车模型,将它绕着旋转中心旋转下列哪个度数后不能与原图形重合.( )
 A、 B、 C、 D、3. 如图,用左面的三角形连续的旋转可以得到右面的图形,每次旋转( )度.
A、 B、 C、 D、3. 如图,用左面的三角形连续的旋转可以得到右面的图形,每次旋转( )度. A、60 B、90 C、120 D、1504. 在线段,正三角形,正方形,平行四边形,等腰梯形,圆六个图形中是中心对称的共有( )A、2个 B、3个 C、4个 D、5个5. 在正三角形、正方形、正五边形和等腰梯形这四种图形中,是旋转对称图形的有( )
A、60 B、90 C、120 D、1504. 在线段,正三角形,正方形,平行四边形,等腰梯形,圆六个图形中是中心对称的共有( )A、2个 B、3个 C、4个 D、5个5. 在正三角形、正方形、正五边形和等腰梯形这四种图形中,是旋转对称图形的有( ) A、1个 B、2个 C、3个 D、4个6. 很多图标在设计时都考虑对称美.下列是几所国内知名大学的图标,若不考虑图标上的文字、字母和数字,其中是中心对称图形的是( )A、
A、1个 B、2个 C、3个 D、4个6. 很多图标在设计时都考虑对称美.下列是几所国内知名大学的图标,若不考虑图标上的文字、字母和数字,其中是中心对称图形的是( )A、 清华大学
B、
清华大学
B、 浙江大学
C、
浙江大学
C、 北京大学
D、
北京大学
D、 中南大学
7. 下列图案中,是中心对称图形的是( )A、
中南大学
7. 下列图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )A、
8. 中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,点A,B,C的对应点分别为A1 , B1 , C1 , 则对称中心E点的坐标是( )
9. 如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,点A,B,C的对应点分别为A1 , B1 , C1 , 则对称中心E点的坐标是( ) A、(3,-1) B、(0,0) C、(2,-1) D、(-1,3)10. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
A、(3,-1) B、(0,0) C、(2,-1) D、(-1,3)10. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、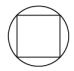 B、
B、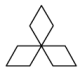 C、
C、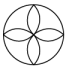 D、
D、
二、填空题
-
11. 规定:在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图),所以正方形是旋转对称图形,且有两个旋转角.
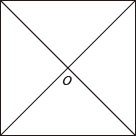
根据以上规定,下列图形是旋转对称图形,也是中心对称图形的是 .
①正五边形;②正六边形;③矩形;④菱形
12. 把一个正六边形绕其中心旋转,至少旋转度,可以与自身重合.13. 如图,在平面直角坐标系中,△A'B'O与△ABO关于坐标原点O中心对称,若点A(2,1)向上平移三个单位可以得到点B,则点B的对应点B′的坐标为. 14. 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
14. 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .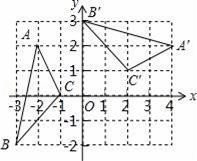 15. 如图,直线、垂直相交于点 , 曲线关于点成中心对称,点的对称点是点 , 于点 , 于点 . 若 , , 则阴影部分的面积之和为 .
15. 如图,直线、垂直相交于点 , 曲线关于点成中心对称,点的对称点是点 , 于点 , 于点 . 若 , , 则阴影部分的面积之和为 .
三、解答题
-
16. 如图,点P是∠AOB外的一点,点Q与P关于OA对称,点R与P关于OB对称,直线QR分别交OA,OB于点M,N,若PM=PN=3,MN=4,求线段QR的长.
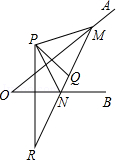 17. 如图所示,O为正六边形的中心,OM是一条折线,交正六边形的一边于点M,你能仅用旋转的方法将此正六边形分成面积相等的六部分吗?如果可以,请作出旋转后的图案.
17. 如图所示,O为正六边形的中心,OM是一条折线,交正六边形的一边于点M,你能仅用旋转的方法将此正六边形分成面积相等的六部分吗?如果可以,请作出旋转后的图案. 18. 如图,该图形是否是轴对称图形?若是,说出它有几条对称轴.它是否是旋转对称图形?若是,说出它旋转多少度能与自身重合.
18. 如图,该图形是否是轴对称图形?若是,说出它有几条对称轴.它是否是旋转对称图形?若是,说出它旋转多少度能与自身重合.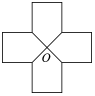 19. 如图,直线m、n相交于点P,且所成的锐角为45°,画出△ABC关于直线m的对称图形△A′B′C′,然后画出△A′B′C′关于直线n的对称图形△A″B″C″,你能发现△ABC与△A″B″C″有什么关系吗?若是平移,指出平移的方向和距离;若是旋转,指出旋转的中心和角度.
19. 如图,直线m、n相交于点P,且所成的锐角为45°,画出△ABC关于直线m的对称图形△A′B′C′,然后画出△A′B′C′关于直线n的对称图形△A″B″C″,你能发现△ABC与△A″B″C″有什么关系吗?若是平移,指出平移的方向和距离;若是旋转,指出旋转的中心和角度. 20. 画图题:(不写画法)
20. 画图题:(不写画法)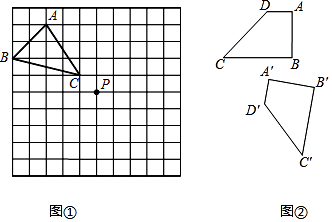 (1)、如图①,在10×10的正方形网格中,每个小正方形的边长为1个单位.请作出△ABC绕点P逆时针旋转90°的△A′B′C′;(2)、如图②,四边形A′B′C′D′是由四边形ABCD绕某一点旋转得到的,请通过作图确定这个点,并把它命名为点O,再把四边形ABCD关于点O的中心对称图形A″B″C″D″画出来.
(1)、如图①,在10×10的正方形网格中,每个小正方形的边长为1个单位.请作出△ABC绕点P逆时针旋转90°的△A′B′C′;(2)、如图②,四边形A′B′C′D′是由四边形ABCD绕某一点旋转得到的,请通过作图确定这个点,并把它命名为点O,再把四边形ABCD关于点O的中心对称图形A″B″C″D″画出来.
21. 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点0为对称中心,画出△ABC关于原点O对称的△A1B1C1 , 并写出A1、B1、C1的坐标.