浙江省温州市浙南名校联盟2021-2022学年高二下学期期末联考数学试题
试卷更新日期:2022-07-15 类型:期末考试
一、单选题
-
1. 设是虚数单位, , 则实数( )A、-2 B、-1 C、1 D、02. 已知全集 , 集合 , 则( )A、 B、 C、 D、3. 若圆锥侧面展开图是圆心角为 , 半径为1的扇形,则这个圆锥表面积与侧面积的比为( )A、3:2 B、2:1 C、4:3 D、5:34. 若正数满足 , 则的最小值为( )A、6 B、 C、 D、5. 已知直线与圆有两个不同的交点,则实数的取值范围是( )A、 B、 C、 D、6. 已知 , 求的值为( )A、 B、 C、 D、7. 在二项式的展开式中只有第5项的二项式系数最大,则展开式中的第4项系数为( )A、7 B、-7 C、 D、8. 已知函数有三个不同的零点(其中),则( )A、1 B、4 C、16 D、64
二、多选题
-
9. 已知数据的平均数为 , 方差为.由这组数据得到新数据 , 其中 , 则( )A、新数据的平均数是 B、新数据的方差是 C、新数据的平均数是 D、新数据的标准差是10. 已知向量 , , 则下列命题不正确的是( )A、若 , 则 B、若在上的投影向量为 , 则向量与夹角为 C、与共线的单位向量只有一个为 D、存在 , 使得11. 在等腰梯形中, , 且 , 以下选项正确的为( )A、 B、等腰梯形外接圆的面积为2π C、若双曲线以为左右焦点,过两点,则其离心率为 D、若椭圆以为左右焦点,过两点,则其离心率为12. 如图,在棱长为的正方体中,点为线段上的动点(含端点),下列四个结论中,正确的有( )
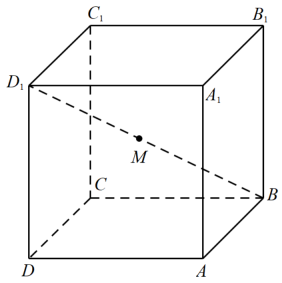 A、存在点 , 使得平面 B、存在点 , 使得直线与直线所成的角为45° C、存在点 , 使得三棱锥的体积为 D、不存在点 , 使得 , 其中为二面角的大小,为直线与直线所成的角
A、存在点 , 使得平面 B、存在点 , 使得直线与直线所成的角为45° C、存在点 , 使得三棱锥的体积为 D、不存在点 , 使得 , 其中为二面角的大小,为直线与直线所成的角三、填空题
-
13. 已知函数是奇函数,则.14. 抛物线的焦点为 , 准线为是抛物线上过焦点的一条直线,且倾斜角为.求线段的值是.15. 设函数 , 其中 , 若存在唯一整数 , 使得 , 则的取值范围是 .16. 在数列的每相邻两项之间插入这两项的和,组成一个新的数列,这样的操作叫做这个数列的一次“拓展”.先将数列1,2进行拓展,第一次拓展得到;第二次拓展得到数列;第次拓展得到数列.设 , 其中 , .
四、解答题
-
17. 已知数列满足(1)、记 , 写出 , 并求出数列的通项公式;(2)、求数列的前2022项和.18. 第24届冬季奥林匹克运动会于2022年2月在北京市和张家口市联合举行.甲、乙是单板滑雪坡面障碍技巧项目的参赛选手,二人在练习赛中均需要挑战3次某高难度动作,每次挑战的结果只有成功和失败两种.(1)、甲在每次挑战中,成功的概率都为0.7.设为甲在3次挑战中成功的次数,求的分布列和数学期望;(2)、乙在第一次挑战时,成功的概率为 , 受心理因素影响,从第二次开始,每次成功的概率会发生改变,其规律为:若前一次成功,则该次成功的概率比前一次成功的概率增加;若前一次失败,则该次成功的概率比前一次成功的概率减少0.1.求乙在3次挑战中有且只有2次成功的条件下,第三次成功的概率.19. 请从下面三个条件中任选一个补充在下面横线上,并作答.
①;②;③.
已知的内角的对边分别是 , 且____.
(1)、求角;(2)、若点为的中点,且 , 试判断的形状.注:如果选择多个条件,按第一个解答计分.