广东省中山市2021-2022学年高二下学期数学期末考试试卷
试卷更新日期:2022-07-15 类型:期末考试
一、单选题
-
1. 袋中有大小相同的红球6个,白球5个,从袋中每次任意取出一个球,直到取出的球是白色为止,所需要的取球次数为随机变量X,则X的可能取值为( )A、1,2,…,6 B、1,2,…,7 C、1,2,…,11 D、1,2,3…2. 某校高二(1)班甲、乙两同学进行投篮比赛,他们进球的概率分别是和 , 现甲、乙各投篮一次,恰有一人进球的概率是( )A、 B、 C、 D、3. 老师想要了解全班50位同学的成绩状况,为此随机抽查了10位学生某次考试的数学与物理成绩,结果列表如下:
学生
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
平均
标准差
数学
88
62
物理
75
63
若这10位同学的成绩能反映全班的成绩状况,且全班成绩服从正态分布,用实线表示全班数学成绩分布曲线,虚线表示全班物理成绩分布曲线,则下列正确的是( )
A、 B、
B、 C、
C、 D、
D、 4. 其食品研究部门为了解一种酒品的储藏年份与芳香度之间的相关关系,在市场上收集到了一部分不同年份的该酒品,并测定了其芳香度(如表).
4. 其食品研究部门为了解一种酒品的储藏年份与芳香度之间的相关关系,在市场上收集到了一部分不同年份的该酒品,并测定了其芳香度(如表).年份
0
1
4
5
6
8
芳香度
1.3
1.8
5.6

7.4
9.3
由最小二乘法得到回归方程 , 但不小心在检测后滴到表格上一滴检测液,污损了一个数据,请你推断该数据为( )
A、6.1 B、6.28 C、6.5 D、6.85. 密位制是度量角与弧的常用制度之一,周角的称为1密位.用密位作为角的度量单位来度量角与弧的制度称为密位制.在密位制中,采用四个数字来记角的密位,且在百位数字与十位数字之间加一条短线,单位名称可以省去,如15密位记为“00—15”,1个平角=30—00,1个周角=60—00,已知函数 , , 当取到最大值时对应的x用密位制表示为( )A、15—00 B、35—00 C、40—00 D、45—006. 已知函数在上单调递增,则实数a的取值范围为( ).A、 B、 C、 D、7. 函数 的图像大致是( )A、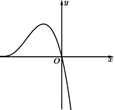 B、
B、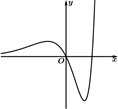 C、
C、 D、
D、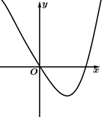 8. 甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军.”对乙说:“你当然不会是最差的.”从这两个回答分析,5人的名次排列方式共有( )种A、54 B、72 C、96 D、120
8. 甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次.甲和乙去询问成绩,回答者对甲说:“很遗憾,你和乙都没有得到冠军.”对乙说:“你当然不会是最差的.”从这两个回答分析,5人的名次排列方式共有( )种A、54 B、72 C、96 D、120二、多选题
-
9. 下列选项中,在 上单调递增的函数有( )A、 B、 C、 D、10. A,B,C,D,E五个人并排站在一起,下列说法正确的是( )A、若A,B不相邻,有72种排法 B、若A在正中间,有24种排法 C、若A在B左边,有24种排法 D、若A,B相邻,有24种排法11. 已知函数的导函数是 , 的图象如图所示,下列说法正确的是( )
 A、函数在上单调递减 B、函数在上单调递减 C、函数在处取得极大值 D、函数共有2个极小值点12. 已知 , , , 则下列结论正确的是( )A、 B、 C、 D、
A、函数在上单调递减 B、函数在上单调递减 C、函数在处取得极大值 D、函数共有2个极小值点12. 已知 , , , 则下列结论正确的是( )A、 B、 C、 D、三、填空题
-
13. 曲线在点处的切线方程为.14. 已知 ,且 ,则 的方差为 .15. 函数的零点个数是 .16. 在一次以“二项分布的性质”为主题的数学探究活动中,立德中学高三某小组的学生表现优异,发现的正确结论得到老师和同学的一致好评.设随机变量 , 记 , .在研究的最大值时,小组同学发现:若为正整数,则时, , 此时这两项概率均为最大值;若为非整数,当取的整数部分,则是唯一的最大值.以此为理论基础,有同学重复投掷一枚质地均匀的骰子并实时记录点数1出现的次数.当投掷到第20次时,记录到此时点数1出现5次,若继续再进行80次投掷试验,则当投掷到第100次时,点数1总共出现的次数为的概率最大.
四、解答题
-
17. 的展开式一共有7项.(1)、求展开式中二项式系数之和;(2)、求展开式中的常数项18. 已知函数在处有极值2.
(Ⅰ)求 , 的值;
(Ⅱ)证明: .
19. 携号转网,也称作号码携带、移机不改号,即无需改变自己的手机号码,就能转换运营商,并享受其提供的各种服务.2019年11月27日,工信部宣布携号转网在全国范围正式启动.某运营商为提质量保客户,从运营系统中选出300名客户,对业务水平和服务水平的评价进行统计,其中业务水平的满意率为 , 服务水平的满意率为 , 对业务水平和服务水平都满意的客户有180人.附: , .
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
(1)、完成下面列联表,并分析是否有97.5%的把握认为业务水平与服务水平有关;对服务水平满意人数
对服务水平不满意人数
合计
对业务水平满意人数
对业务水平不满意人数
合计
(2)、为进一步提高服务质量.在选出的对服务水平不满意的客户中,抽取2名征求改进意见,用X表示对业务水平不满意的人数,求X的分布列与期望.20. 如图,在正三棱锥中,有一半径为1的半球,其底面圆O与正三棱锥的底面贴合,正三棱锥的三个侧面都和半球相切.设点D为BC的中点, . (1)、用分别表示线段BC和PD长度;(2)、当时,求三棱锥的侧面积S的最小值.21. 某机构为研究考生物理成绩与数学成绩之间的关系,从一次考试中随机抽取11名考生的数据,统计如下表:
(1)、用分别表示线段BC和PD长度;(2)、当时,求三棱锥的侧面积S的最小值.21. 某机构为研究考生物理成绩与数学成绩之间的关系,从一次考试中随机抽取11名考生的数据,统计如下表:数学成绩
46
65
79
89
99
109
110
116
123
134
140
物理成绩
50
54
60
63
66
68
0
70
73
76
80
(1)、由表中数据可知,有一位考生因物理缺考导致数据出现异常,剔除该组数据后发现,考生物理成绩与数学成绩之间具有线性相关关系,请根据这10组数据建立关于的回归直线方程,并估计缺考考生如果参加物理考试可能取得的成绩;(2)、已知参加该次考试的10000名考生的物理成绩服从正态分布 , 用剔除异常数据后的样本平均值作为的估计值,用剔除异常数据后的样本标准差作为的估计值,估计物理成绩不低于75分的人数的期望.附:参考数据:
1110
660
68586
120426
4770
0.31
上表中的;表示样本中第名考生的数学成绩,;表示样本中第名考生的物理成绩,.参考公式:①对于一组数据: , 其方差:.②对于一组数据 , 其回归直线的斜率和截距的最小二乘估计分别为: , .③若随机变量服从 , 则 , , .
22. 已知函数.(1)、证明:当时,;(2)、从编号为1~100的100张卡片中每次随机抽取一张,然后放回,用这种方式连续抽取20张,设抽取的20个号码互不相同的概率为.证明:.