（沪教版）2022-2023学年度第一学期七年级数学11.1 平移同步测试

试卷更新日期：2022-07-15 类型：同步测试

进入出卷网下载

一、单选题

1. 数轴上一点 $a$ 表示的有理数为-5，若将 $a$ 点向右平移4个单位长度，则此时 $a$ 点表示的有理数为（）

A、-5 B、4 C、1 D、-1

查看试题解析
2. 点A在数轴上表示+2，将点A沿数轴向左平移3个单位长度到点B，则点B表示的数是（）

A、-1 B、3 C、5． D、-1或3

查看试题解析
3. 在平面直角坐标系中，将点A(-1，-2)向右平移3个单位长度得到点B，则点B的坐标为（）

A、(-1，1) B、(2，-2) C、(-4，-2) D、(-1，-5)

查看试题解析
4. 平面直角坐标系中，一个图案上各个点的横坐标都乘以 $- 1$ ，纵坐标不变，得到一个图案，下列结论正确的是（　　　）

A、新图案是原图案向下平移了 $1$ 个单位 B、新图案是原图案向左平移了 $1$ 个单位 C、新图案与原图案关于x轴对称 D、新图案与原图案形状和大小完全相同

查看试题解析
5. 如图， $△ A B C$ 沿射线 $B C$ 方向平移到 $△ D E F$ （点E在线段 $B C$ 上），如果 $B C = 8 cm$ ， $E C = 5 cm$ ，那么平移距离为（）

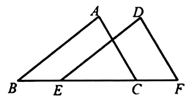A、3cm B、5cm C、8cm D、13cm

查看试题解析
6. 如图所示，从A到B有 $① ② ③$ 三条路可以走，每条路长分别为L，M，N，则L，M，N的大小关系是 $()$ ．

A、 $L > M > N$ B、 $L = M > N$ C、 $M > N > L$ D、 $L > N > M$

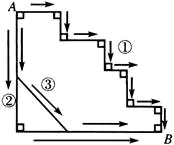查看试题解析
7. 数轴上一动点 A 向左移动2个单位长度到达点 B ，再向右移动6个单位长度到达点 C ，若点 C 表示的数是1，则点 A 表示的数为（）

A、7 B、3 C、-3 D、-2

查看试题解析
8. 数轴上一点A表示的数是-2，将点A先向左移动3个单位长度到达点 $B$ ，再向右移动 $7$ 个单位长度到达点C ，则点C表示的数是（）

A、1 B、2 C、-1 D、-2

查看试题解析
9. 数轴上点A表示的数是 $- 3$ ，将点A在数轴上平移 $7$ 个单位长度得到点B.则点B表示的数是（）

A、 $4$ B、 $- 4$ 或 $10$ C、 $- 10$ D、 $4$ 或 $- 10$

查看试题解析
10. 若数轴上的点A向左移动2个单位长度，再向右移动3个单位长度，正好对应-5这个点，那么原来A对应的数是（）．

A、-4 B、2 C、-6 D、0

查看试题解析

二、填空题

11. 点A在数轴上距原点3个单位长度，若一个点从点A处先向右移动5个单位长度，再向左移动1个单位长度，此时所表示的数是

查看试题解析
12. 若把一个边长为2厘米的等边 $△ A B C$ 向右平移a厘米，则平移后所得三角形的周长为厘米．

查看试题解析
13. 已知线段AB的长度为3厘米，现将线段AB向左平移4厘米得到线段CD，那么线段CD的长度为厘米．

查看试题解析
14. 今欲在运动会颁奖台上面及两侧铺上地毯(如图斜线部分)，则需要cm²的地毯.

查看试题解析
15. 数轴上的点A表示-3，将点A先向右移动7个单位长度，再向左移动5个单位长度，那么终点到原点的距离是个单位长度．

查看试题解析

三、解答题

16. 如图，在边长为1的小正方形组成的网格中， $△ A B C$ 的顶点在格点（网格线的交点）上，以点 $O$ 为原点建立平面直角坐标系，点 $B$ 的坐标为（1，0）.

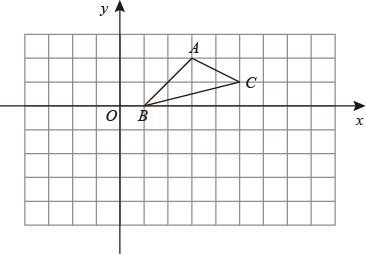
（ 1 ）将 $△ A B C$ 向左平移5个单位长度，得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ；

（ 2 ）以点 $O$ 为位似中心，将 $△ A_{1} B_{1} C_{1}$ 放大到两倍（即新图与原图的相似比为2），得到 $△ A_{2} B_{2} C_{2}$ ，在所给的方格纸中画出 $△ A_{2} B_{2} C_{2}$ ；

（ 3 ）若点 $M$ 是 $A B$ 的中点，经过（1）、（2）两次变换， $M$ 的对应点 $M_{2}$ 的坐标是 .

查看试题解析
17. 如图，平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为 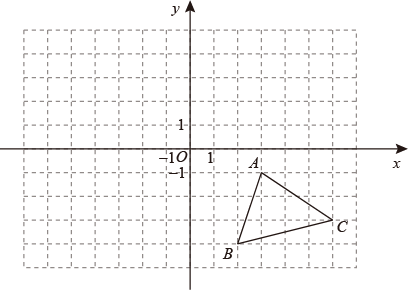$A (3 ， - 1)$ ， $B (2 ， - 4)$ ， $C (6 ， - 3)$ ．
（ 1 ）请在图中画出与 $△ A B C$ 关于原点成中心对称的 $△ A_{1} B_{1} C_{1}$ ，并直接写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标： $A_{1}$ ▲ ， $B_{1}$ ▲ ， $C_{1}$ ▲ ；
（ 2 ）将点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的横坐标分别加5，纵坐标分别减2，依次得到点 $A_{2}$ ， $B_{2}$ ， $C_{2}$ ，请在图中画出 $△ A_{2} B_{2} C_{2}$ ；
（ 3 ）若点 $P (m ， n)$ 是 $△ A B C$ 内的任意一点，点P经过（1）（2）中的两次变换后的对应点为 $P_{2}$ ，则点 $P_{2}$ 的坐标为 ▲ （用含m，n的式子表示）．

查看试题解析
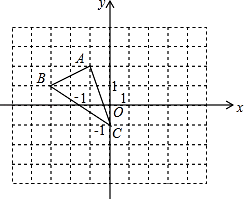
18. 在平面直角坐标系中，把点P（－5，4）向右平移9个单位得到点P₁ ，再将点P₁绕原点逆时针旋转90°得到点P₂ ，求点P₂的坐标．

查看试题解析
19. 在如图所示的网格中建立平面直角坐标系， $△ A B C$ 的顶点在网格线的交点上，点 $B$ 的坐标为 $(- 1 ， - 1)$ ．

(1)、画出 $△ A B C$ 向上平移4个单位长度得到的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $B$ 的对应点 $B_{1}$ 的坐标；

(2)、画出 $△ A_{1} B_{1} C_{1}$ 绕原点 $O$ 顺时针旋转90°得到的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $B_{1}$ 的对应点 $B_{2}$ 的坐标．

查看试题解析
20. 如图，已知三角形ABC中，∠ABC=90°，边BC=12cm，把三角形ABC向下平移至三角形DEF后，AD=5cm，GC=4cm，请求出图中阴影部分的面积。

查看试题解析
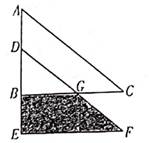21. 在平面直角坐标系中，△ABC的位置如图所示，三个顶点的坐标分别为：A（1，2）、B（2，3）、C（3，0）．

⑴现将△ABC先向左平移5个单位长度，再向上平移2个单位长度，得到△A₁B₁C₁ ，请在平面直角坐标系中画出△A₁B₁C₁ ．

⑵此时平移的距离是多少；

⑶在平面直角坐标系中画出△ABC关于点O成中心对称的△A₂B₂C₂ ．

查看试题解析
22. 如图，四边形 $A B C D$ 是平行四边形， $A D = 6$ ， $A B = 8$ ，点 $A$ 的坐标为 $(- 3 ， 0)$ ，求点 $B$ 、 $C$ 、 $D$ 的坐标.

查看试题解析
23. 在平面直角坐标系中，已知△ABC的顶点坐标分别是A（﹣1，2）、B（﹣3，1）、C（0，﹣1）．

(1)、将△ABC向左平移4个单位，得到△A₁B₁C₁ ，画出平移后的图形；

(2)、将△ABC绕点C按顺时针方向旋转90°后得到△A₂B₂C，画出△A₂B₂C．并写出A对应点A₂坐标．

查看试题解析
24. 如图，三角形 $A B C$ 是由三角形 $D E F$ 经过某种变换得到的，观察对应点 $A$ 与 $D$ ， $B$ 与 $E$ ， $C$ 与 $F$ 的坐标变化，说明三角形 $A B C$ 是由三角形 $D E F$ 经过怎样的变换得到的.

查看试题解析

（沪教版）2022-2023学年度第一学期七年级数学11.1 平移 同步测试

一、单选题

二、填空题

三、解答题

（沪教版）2022-2023学年度第一学期七年级数学11.1 平移同步测试