(沪教版)2022-2023学年度第一学期七年级数学9.12 完全平方公式 同步测试
试卷更新日期:2022-07-15 类型:同步测试
一、单选题
-
1. 多项式x2+A+1是个完全平方式,那么代数式A不可能为( )A、2x B、x C、﹣2x D、x42. 下列运算正确的是( )A、(m+n)(﹣m+n)=n2﹣m2 B、(a﹣b)2=a2﹣b2 C、(a+m)(b+n)=ab+mn D、(x﹣1)2=x2﹣2x﹣13. 如果 2+2m +16是一个完全平方式,则m的值是( )A、4 B、8 C、 4 D、 84. 已知 .则xy=( )A、8 B、9 C、10 D、115. 已知 ,则 的值为( )A、 B、 C、 D、6. 如图,对一个正方形进行了分割,通过面积恒等,能够验证下列哪个等式( )
 A、 B、 C、 D、7. 下列乘法中,能运用完全平方公式进行运算的是( )A、(x+a)(x-a) B、(b+m)(m-b) C、(-x-b)(x-b) D、(a+b)(-a-b)8. 如果 ,那么a.b的值分别为( )A、2;4 B、5;-25 C、-2;25 D、-5;259. 已知x+y=5,x²+y²=13,那么xy的值是 ( )A、12 B、 C、6 D、10. 要使 成为一个完全平方式,则 的值是( )A、
A、 B、 C、 D、7. 下列乘法中,能运用完全平方公式进行运算的是( )A、(x+a)(x-a) B、(b+m)(m-b) C、(-x-b)(x-b) D、(a+b)(-a-b)8. 如果 ,那么a.b的值分别为( )A、2;4 B、5;-25 C、-2;25 D、-5;259. 已知x+y=5,x²+y²=13,那么xy的值是 ( )A、12 B、 C、6 D、10. 要使 成为一个完全平方式,则 的值是( )A、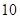 B、
B、 C、20
D、
C、20
D、
二、填空题
-
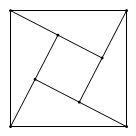
11. 已知 ,则 .12. 已知 ,则代数式 的值是 .13. 如果(a+ )2=a2+6ab+9b2 , 那么括号内可以填入的代数式是 . (只需填写一个)14. 已知 满足 ,则 的值是 .15. “赵爽弦图”巧妙的利用面积证明了勾股定理.如图所示的“赵爽弦图”是用四个全等的直角三角形和一个小正方形拼成一个大正方形.若直角三角形两直角边分别为 , ,且 ,大正方形的面积为 ,则 .
三、解答题
-
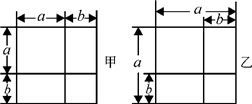
16. 已知a=﹣ ,b=3,试求代数式4a2﹣12ab+9b2的值.17. 已知: , ,求 和 的值.18. 利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2 . 你根据图乙能得到的数学公式是怎样的?写出得到公式的过程.
 19.
19.
(1)、按下表已填写的完成表中的空白处代数式的值:4
16
(2)、比较表中两代数式计算结果,请写出你发现 与 有什么关系?(3)、利用你发现的结论,求 。20. ① ,②
,② 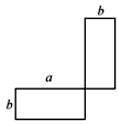 ,③
,③ 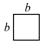 ,④
,④ 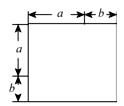 (1)、在下列横线上用含有a,b的代数式表示相应图形的面积.
(1)、在下列横线上用含有a,b的代数式表示相应图形的面积.①;②;③;④ .
(2)、通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:;(3)、利用(2)的结论计算992+2×99×1+1的值.四、综合题
-
21.(1)、在下列横线上用含有a,b的代数式表示相应图形的面积.
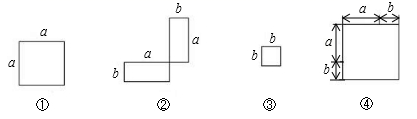
①a2;②. ③b2 ; ④.
(2)、请在图④画出拼图并通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达:.(3)、利用(2)的结论计算10.232+20.46×9.77+9.772的值.22. 用字母表示数,字母和数一样参与运算,可以用式子把数量关系简明地表示出来,有助于我们探索和发现更多有趣的数学规律.(1)、完善表格与 和的平方
、 两数的平方和加上 、 两数的积的2倍
用代数式表示
▲
,
1
/
,
25
▲
,
/
9
…
…
…
根据表中计算结果,你有什么发现?
(2)、根据你发现的规律,计算 .