（沪教版）2022-2023学年度第一学期七年级数学9.11 平方差公式同步测试

试卷更新日期：2022-07-14 类型：同步测试

进入出卷网下载

一、单选题

1. 下列各式中，能用平方差公式计算的是（）

A、（a+b）（﹣a﹣b） B、（a+b）（a﹣b） C、（a+b）（a﹣d） D、（a+b）（2a﹣b）

查看试题解析
2. 记 $x = (1 + 2) (1 + 2^{2}) (1 + 2^{4}) (1 + 2^{8}) \dots (1 + 2^{n})$ ，且 $x + 1 = 2^{128}$ ，则 $n =$ （）．

A、128 B、32 C、64 D、16

查看试题解析
3. 如图，在边长为a的正方形中挖掉一个边长为b的小正方形，把余下的部分拼成一个长方形（无重叠部分），通过计算两个图形中阴影部分的面积，可以验证的一个等式是（）

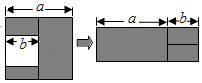A、a²﹣b²＝（a+b）（a﹣b） B、a（a﹣b）＝a²﹣ab C、（a﹣b）²＝a²﹣2ab+b² D、a（a+b）＝a²+ab

查看试题解析
4. 如图，从边长为(a＋1)cm的正方形纸片中剪去一个边长为(a－1)cm的正方形(a>1)，剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙)，则长方形的长为（）

A、2 cm B、2a cm C、4a cm D、(2a－2)cm

查看试题解析
5. 如图(1)，在边长为 $a$ 的大正方形中，剪去一个边长为 $b (a > b)$ 的小正方形，然后将余下的部分剪开拼成长方形，如图(2)，若大正方形的周长为 $c_{1} ，$ 长方形的周长为 $c_{2} ，$ 则 $c_{1}$ 与 $c_{2}$ 的大小关系是

A、 $c_{1} > c_{2}$ B、 $c_{1} = c_{2}$ C、 $c_{1} < c_{2}$ D、不能确定

查看试题解析
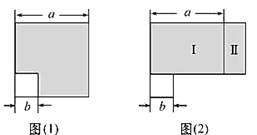6. 一个自然数若能表示为两个自然数的平方差，则称这个自然数为“智慧数”，比如99=10²-1² ，故99是一个智慧数．在下列各数中，不属于“智慧数”的是（）

A、15 B、16 C、17 D、18

查看试题解析
7. 如图，从边长为 $(a + 4) c m$ 的大正方形纸片中剪去一个边长为 $(a + 1) c m$ 的小正方形 $(a > 0)$ ，剩余部分沿虚线剪开，拼成一个矩形（不重叠无缝隙），则矩形的面积为（）

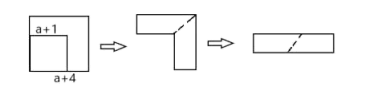A、 $a (2 a + 5) c m^{2}$ B、 $3 (2 a + 5) c m^{2}$ C、 $3 (2 a + 1) c m^{2}$ D、 $a (2 a + 1) c m^{2}$

查看试题解析
8. 已知a﹣b=3，则a²﹣b²﹣6b的值为（）

A、9 B、6 C、3 D、﹣3

查看试题解析
9. 在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图1），把余下的部分拼成一个矩形（如图2），根据两个图形中阴影部分的面积相等，可以验证（）

A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $a (a - b) = a^{2} - a b$

查看试题解析
10. 如图所示，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（）

A、（a﹣b）²=a²﹣2ab+b² B、（a+b）²=a²+2ab+b² C、a²﹣b²=（a+b）（a﹣b） D、a²+ab=a（a+b）

查看试题解析

二、填空题

11. 100²﹣99²＋98²﹣97²＋96²﹣95²＋…＋2²﹣1²＝．

查看试题解析
12. 根据公式x²﹣y²＝（x+y）（x﹣y）来解题有时能起到简化计算的效果.比如计算50²﹣49＝（50+49）×（50﹣49）＝99×1＝99，根据这种方法计算（ $\frac{9}{11}$ ）²﹣（ $\frac{2}{11}$ ）²结果是

查看试题解析
13. 计算 $\frac{6058}{3} \times \frac{6062}{3} - 2020^{2}$ ＝．

查看试题解析
14. 如图，边长为（m＋3）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个长方形（不重叠无缝隙），若拼成的长方形一边长为3，则另一边长是．

查看试题解析
15. $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) ...... (1 - \frac{1}{1999^{2}}) (1 - \frac{1}{2000^{2}})$ = ．

查看试题解析

三、解答题

16. 分解因式: ${(3 m - 1)}^{2} - {(2 m - 3)}^{2}$ .

查看试题解析
17. 已知圆环的面积为 $π$ ，其中大圆与小圆周长的和为 $4 π$ ，求圆环的宽度（大圆半径与小圆半径的差）.

查看试题解析

四、综合题

18. 填表并回答问题：
x
1
1
0
2
y
2
3
3
1
（x+y）（x﹣y）
x²﹣y²

(1)、观察并填出表，你有何发现，将你的发现写在横线上：．

(2)、利用你发现的结果计算：2022²﹣2021² ．

查看试题解析
19.

(1)、如图1所示，若大正方形的边长为 $a$ ，小正方形的边长为 $b$ ，则阴影部分的面积是；若将图1中的阴影部分裁剪下来，重新拼成如图2所示的一个长方形，则它的面积是；

(2)、由（1）可以得到一个乘法公式是；

(3)、利用你得到的公式计算： $202 1^{2} - 2022 \times 2020$ ．

查看试题解析
20. 实践与探索
如图1，边长为 $a$ 的大正方形有一个边长为 $b$ 的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示）

(1)、上述操作能验证的等式是____；（请选择正确的一个）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 $a^{2} - 2 a b + b^{2} = {(a - b)}^{2}$ C、 $a^{2} + a b = a (a + b)$

(2)、请应用这个公式完成下列各题：
①已知 $4 a^{2} - b^{2} = 24$ ， $2 a + b = 6$ ，则 $2 a - b =$ ▲ ．
②计算： $10 0^{2} - 9 9^{2} + 9 8^{2} - 9 7^{2} + ⋯ + 4^{2} - 3^{2} + 2^{2} - 1^{2}$

查看试题解析
21. 当 $a = 4 ， b = - 5$ 时，求下列代数式的值

(1)、 $a^{2} - b^{2}$

(2)、 $(a + b) (a - b)$

(3)、观察上述两个代数式的值有什么关系？

(4)、请用简便的方法计算出 $202 1^{2} - 202 0^{2}$ 的值

查看试题解析
22. 如图，一个长方形运动场被分隔成 $A ， B ， A ， B ， C$ 共5个区， $A$ 区是边长为 $a m$ 的正方形， $C$ 区是边长为 $b m$ 的正方形.

(1)、列式表示整个长方形运动场的面积，并将式子化简

(2)、如果 $a = 50 ， b = 30$ ，求整个长方形运动场的面积.

查看试题解析
23. 在边长为a的正方形的一角减去一个边长为 $b$ 的小正方形（ $a > b$ ），如图①

(1)、由图①得阴影部分的面积为；

(2)、沿图①中的虚线剪开拼成图②，则图②中阴影部分的面积为；

(3)、由（1）（2）的结果得出结论：=；

(4)、利用（3）中得出的结论计算： $2020^{2} - 2019^{2}$

查看试题解析
24. 如图，两个边长分别为a、b（ $a$ > $b$ ）的正方形纸片叠放在一起．（用含有a、b的代数式表示问题的结果）

(1)、请用至少两种方法求出图中阴影部分的面积；

(2)、由面积相等，你发现了怎样的等量关系？

查看试题解析

x	1	1	0	2
y	2	3	3	1
（x+y）（x﹣y）
x²﹣y²

（沪教版）2022-2023学年度第一学期七年级数学9.11 平方差公式 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（沪教版）2022-2023学年度第一学期七年级数学9.11 平方差公式同步测试