（沪教版）2022年暑假六年级数学复习巩固专题18 长方体的再认识

试卷更新日期：2022-07-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列说法中，
⑴联结两点的线段叫做两点之间的距离；（2）用度量法和叠合法都可以比较两个角的大小；（3）铅垂线、三角尺、合页型折纸都可以检验直线和平面垂直：（4）六个面、十二条棱和八个顶点组成的图形都是长方体；你认为正确的个数为…（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列说法中正确的是（）

A、四棱锥有4个面 B、连接两点间的线段叫做两点间的距离 C、如果线段 $A M = B M$ ，则M是线段AB的中点 D、射线 $A B$ 和射线 $B A$ 不是同一条射线

查看试题解析
3. 将自然数1至6分别写在一个正方体的6个面上，然后把任意相邻两个面上的数之和写在这两个面的公共棱上．则在这个正方体中所有棱上不同数的个数的最小值和最大值分别是（）

A、7，9 B、6，9 C、7，10 D、3，11

查看试题解析
4. 下列说法：①两点之间的所有连线中，线段最短；②相等的角是对顶角；③过一点有且仅有一条直线与已知直线平行；④长方体是四棱柱；其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，长方体的长为20cm，宽为15cm，高为10cm，点B离点C为5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖，需要爬行的最短距离是（）

A、 $5 \sqrt{29}$ B、25 C、 $5 \sqrt{37}$ D、16

查看试题解析
6. 某长方体的展开图中， $P 、 A 、 B 、 C 、 D$ (均为格点)的位置如图所示，一只蚂蚁从点 $P$ 出发，沿着长方体表面爬行.若此蚂蚁分别沿最短路线爬行到 $A 、 B 、 C 、 D$ 四点，则蚂蚁爬行距离最短的路线是（）

A、 $P \to A$ B、 $P \to B$ C、 $P \to C$ D、 $P \to D$

查看试题解析
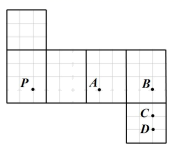7. 如图所示，有一个长、宽各2米，高为3米且封闭的长方体纸盒，一只昆虫从顶点A要爬到顶点B，那么这只昆虫爬行的最短路程为（）

A、3米 B、4米 C、5米 D、6米

查看试题解析
8. 如图是放在地面上的一个长方体盒子，其中AB=9cm，BC=6cm，BF=5cm，点M在棱AB上，且AM=3cm，点N是FG的中点，一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程为（）

A、10cm B、 $\sqrt{106} c m$ C、 $（ 6 + \sqrt{34} ） c m$ D、9cm

查看试题解析
9. 如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是（）

A、5 $\sqrt{21}$ B、25 C、10 $\sqrt{5}$ +5 D、35

查看试题解析

二、填空题

10. 如图是以长为120cm，宽为80cm的长方形硬纸，在它的四个角处各剪去一个边长为20cm的正方形后，将其折叠成如图所示的无盖的长方体，则这个长方体的体积为．

查看试题解析
11. 如图，长方体中， $AB = 12 m$ ， $BC = 2 m$ ， $BB^{'} = 3 m$ ，一只蚂蚁从点A出发，以4m/秒的速度沿长方体表面爬行到点C'，至少需要分钟.

查看试题解析
12. 如图，长方体的底面边长分别为2cm和4cm，高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为cm.

查看试题解析
13. 在一个长为8分米，宽为5分米，高为7分米的长方体上，截去一个长为6分米，宽为5分米，深为2分米的长方体后，得到一个如图所示的几何体. 一只蚂蚁要从该几何体的顶点A处，沿着几何体的表面到几何体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是分米．

查看试题解析

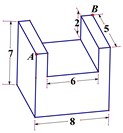
三、解答题

14. 底面半径为10cm，高为40cm的圆柱形水桶中装满了水。小明先将桶中的水倒满3个底面半径为3cm，高为5cm的圆柱形杯子，如果剩下的水倒在长、宽、高分别为50cm，20cm和12cm的长方体容器内，会满出来吗？若没有满出来，求出长方体容器内水的高度（ $π$ 取3）。

查看试题解析
15. 如图所示，是一个长方体纸盒平面展开图，已知纸盒中相对两个面上的数互为相反数．求a，b，c的值？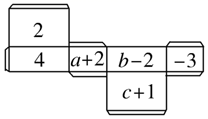

查看试题解析
16. 如图，长方体的长为15，宽为10，高为20，点B离点C的距离是5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是多少？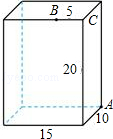

查看试题解析

四、综合题

17. 一个小立方体的六个面分别标有字母A，B，C，D，E，F，从三个不同方向看到的情形如图所示.

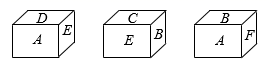(1)、A对面的字母是， B对面的字母是， E对面的字母是.（请直接填写答案）

(2)、若A=2x-1， $B = - 3 x + 9$ ， C=-7，D=1，E=2x＋5，F= -9，且字母E与它对面的字母表示的数互为相反数，求A，B的值.

查看试题解析
18. 如图所示，某品牌 $1 L$ 的牛奶包装盒，高 $25 c m$ ，底面为长方形，将包装剪开铺平，得到如图的纸样.

(1)、牛奶包装盒底面长方形的长和宽分别是多少？

(2)、若不改变牛奶盒的容积和高度，将生奶盒的底面改为正方形，能否节约包装盒的纸张面积？若能，请计算每个生奶盒可节约的纸张面积；若不能，请说明理由.

查看试题解析
19. 如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．

(1)、填空： a= ， b= ， c=；

(2)、先化简，再求值： $5 a^{2} b - [2 a^{2} b - 3 (2 a b c - a^{2} b) + 4 a b c]$ ．

查看试题解析
20. 一个正方体的六个面分别标有字母A、B、C、D、E、F，从三个不同方向看到的情形如图所示．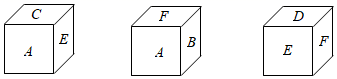

(1)、A的对面是， B的对面是， C的对面是；（直接用字母表示）

(2)、若A＝﹣2，B＝|m﹣3|，C＝m﹣3n﹣ $\frac{11}{2}$ ， E＝（ $\frac{5}{2}$ +n）² ，且小正方体各对面上的两个数都互为相反数，请求出F所表示的数．

查看试题解析
21. 仔细阅读，解答下列问题

(1)、有一长方体的食物包装纸盒如图(1)，已知长方体的底面长为12，宽为9，高为5，一只蚂蚁想从底面A处爬到B处去吃食物，请问：蚂蚁爬行的最短距离是多少?

(2)、如图(2)，圆柱形容器的高为1.2米，底面周长为1米，在容器内壁高容器底部0.3米的点B处有一只蚊子，此时一只壁虎正好在容器外壁高容器上沿0.3米与蚊子相对的点A处，求壁虎捕捉到蚊子的最短路程是多少?(容器厚度忽略不计)

查看试题解析
22. 图1、图2为同一长方体房间的示意图，图3为该长方体的表面展开图．

(1)、蜘蛛在顶点A′处．
①苍蝇在顶点B处时，试在图1中画出蜘蛛为捉住苍蝇，沿墙面爬行的最近路线．
②苍蝇在顶点C处时，图2中画出了蜘蛛捉住苍蝇的两条路线，往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC，试通过计算判断哪条路线更近．

(2)、在图3中，半径为10dm的⊙M与D′C′相切，圆心M到边CC′的距离为15dm，蜘蛛P在线段AB上，苍蝇Q在⊙M的圆周上，线段PQ为蜘蛛爬行路线，若PQ与⊙M相切，试求PQ长度的范围．

查看试题解析