江苏省镇江市2021-2022学年七年级下学期期中数学试卷
试卷更新日期:2022-07-14 类型:期中考试
一、填空题
-
1. 计算: =.2. 一个多边形的内角和是1800°,则这个多边形的边数为 .3. 熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播.经测量,医用外科口罩的熔喷布厚度约为0.000156米,将0.000156用科学记数法表示应为.4. 如图所示,a//b,∠1=130°,则∠ 2的度数是.
 5. 因式分解: =.6. 三角形的三边长为2,a,5,如果这个三角形中有两条边相等,那么它的周长是.7. 若是一个完全平方式,则常数的值为.8. 如图,将一副直角三角板,按如图所示叠放在一起,则图中∠COB=.
5. 因式分解: =.6. 三角形的三边长为2,a,5,如果这个三角形中有两条边相等,那么它的周长是.7. 若是一个完全平方式,则常数的值为.8. 如图,将一副直角三角板,按如图所示叠放在一起,则图中∠COB=.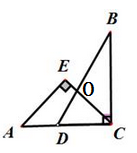 9. 如图,直线m∥n,∠AOB的两边分别于直线n、m交于点A、B,已知∠AOB=120°,则∠2﹣∠1=.
9. 如图,直线m∥n,∠AOB的两边分别于直线n、m交于点A、B,已知∠AOB=120°,则∠2﹣∠1=. 10. 若 , 则.11. 如图,已知∠A+∠B+∠C+∠D=230°,则∠CED=°.
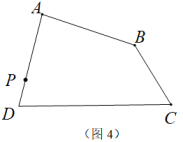
10. 若 , 则.11. 如图,已知∠A+∠B+∠C+∠D=230°,则∠CED=°. 12. 如图,将△ABC沿BC方向平移到△DEF(B、E、F在同一条直线上),若∠B=46°,AC与DE相交于点G,∠AGD和∠DFB的平分线GP、FP相交于点P,则∠P=°.
12. 如图,将△ABC沿BC方向平移到△DEF(B、E、F在同一条直线上),若∠B=46°,AC与DE相交于点G,∠AGD和∠DFB的平分线GP、FP相交于点P,则∠P=°.
二、单选题
-
13. 下列计算正确的是( )A、 B、 C、 D、14. 下列各式中,不能用平方差公式计算的是( )A、(2x﹣y)(2x + y) B、(x﹣y)(﹣y﹣x) C、(b﹣a)(b + a) D、(﹣2x + y)(2x﹣y)15. 如图,在△ABC中,BC边上的高为( )
 A、AD B、BE C、BF D、CG16. 如图,下列条件中:不能判定AB//CD的条件是( )
A、AD B、BE C、BF D、CG16. 如图,下列条件中:不能判定AB//CD的条件是( ) A、∠B+∠BCD=180° B、∠1=∠2 C、∠3=∠4 D、∠B=∠517. 已知a﹣b=2,则a2﹣b2﹣4b的值为( )A、5 B、4 C、2 D、118. 如图,C是线段AB上的一点,分别以AC,BC为边在同侧作正方形,若AB=8,两正方形的面积和为48,则△AFC的面积是( )
A、∠B+∠BCD=180° B、∠1=∠2 C、∠3=∠4 D、∠B=∠517. 已知a﹣b=2,则a2﹣b2﹣4b的值为( )A、5 B、4 C、2 D、118. 如图,C是线段AB上的一点,分别以AC,BC为边在同侧作正方形,若AB=8,两正方形的面积和为48,则△AFC的面积是( ) A、8 B、6 C、4 D、2
A、8 B、6 C、4 D、2三、解答题
-
19. 计算与化简:(1)、(2)、(3)、(4)、20. 因式分解:(1)、x2﹣9(2)、2a(x-y)+b(y-x)(3)、x3y-6x2y+9xy21. 数学课上老师与同学们一起利用球的体积公式计算出地球的体积约是立方千米,接着老师问道:“科学家们正在寻找一颗星球,也可以近似地看做球体,它的半径是地球的10000倍,那么这样的星球它的体积约是多少立方千米?”请你尝试计算.22. 如图,在每个小正方形的边长为1的方格纸中,△ABC的顶点都在格点上,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B'.
 (1)、利用网格画出△ABC的高AD;(2)、在方格纸中画出平移后的△A′B′C′;(3)、在△ABC平移到△A′B′C′的过程中,线段BC扫过的面积为 .23. 如图,已知直线AB∥CD,∠B=50°,∠BEC=25°,EC平分∠BEF.
(1)、利用网格画出△ABC的高AD;(2)、在方格纸中画出平移后的△A′B′C′;(3)、在△ABC平移到△A′B′C′的过程中,线段BC扫过的面积为 .23. 如图,已知直线AB∥CD,∠B=50°,∠BEC=25°,EC平分∠BEF. (1)、请说明AB∥EF的理由;(2)、求∠DCE的度数.24. 阅读材料:怎样证实“两直线平行,同位角相等”
(1)、请说明AB∥EF的理由;(2)、求∠DCE的度数.24. 阅读材料:怎样证实“两直线平行,同位角相等”本节中,我们用叠合的方法发现了“两直线平行,同位角相等” .事实上,这个结论可以运用已有的基本事实,通过说理加以证实.
如图,直线AB、CD被直线EF所截,AB//CD,∠1与∠2是同位角.
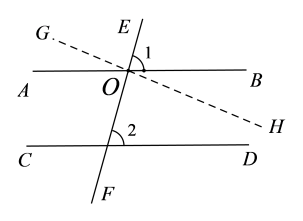
假设∠1∠2,那么可以通过直线AB与EF的交点O作直线GH,使∠EOH=∠2,直线GH与直线AB是两条直线.
根据基本事实“同位角相等,两直线平行”,由∠EOH=∠2,可以得到GH//CD.
这样,过点O就有两条直线AB、GH都与CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.
这说明∠1∠2的假设不正确,于是∠1=∠2.
解决问题:若且 , 请你用以上方法说明:.
25. 一天小明和小丽玩纸片拼图游戏,他们发现利用图1中的三种类型的纸片可以拼出一些图形来解释某些等式,例如,由图2,我们可以得到.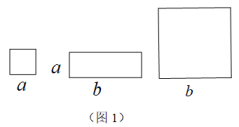


 (1)、由图3可以解释的等式是;(2)、用边长为a的正方形卡片1张,边长分别为a,b的长方形卡片6张,边长为b的正方形卡片9张,用这16张卡片拼成一个正方形,则这个正方形的边长为;(3)、小丽用5个长为b,宽为a的长方形按照图4方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分,设左上角的面积为S1 , 右下角的面积为S2 , 当BC的长变化时,S2﹣S1的值始终保持不变,求a与b的数量关系.26.(1)、【问题提出】在△ABC中,点P是线段BC的中点.在图1中,过点P画一条直线平分△ABC的面积.(2)、【问题探究】育才中学“思维畅想”社团的同学们又研究了这样一个问题:如图2,在△ABC中,点P是线段BC的中点.若点E是线段BP上一点(不与点B、P重合),能否过E作直线平分△ABC的面积?小明给出了如下画法:
(1)、由图3可以解释的等式是;(2)、用边长为a的正方形卡片1张,边长分别为a,b的长方形卡片6张,边长为b的正方形卡片9张,用这16张卡片拼成一个正方形,则这个正方形的边长为;(3)、小丽用5个长为b,宽为a的长方形按照图4方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分,设左上角的面积为S1 , 右下角的面积为S2 , 当BC的长变化时,S2﹣S1的值始终保持不变,求a与b的数量关系.26.(1)、【问题提出】在△ABC中,点P是线段BC的中点.在图1中,过点P画一条直线平分△ABC的面积.(2)、【问题探究】育才中学“思维畅想”社团的同学们又研究了这样一个问题:如图2,在△ABC中,点P是线段BC的中点.若点E是线段BP上一点(不与点B、P重合),能否过E作直线平分△ABC的面积?小明给出了如下画法:
作线段AC的中点D;(2)连接DE、BD;(3)过B作BMDE交AC于点M;(4)连接EM,则直线EM平分△ABC的面积.小明画法正确吗?请你说明理由.
(3)、【问题延伸】在四边形ABCD中,点P是AD上一点,请选择图3或图4过点P作直线PQ平分四边形ABCD的面积.