江苏省无锡市惠山区2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-07-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、a＋2a＝3a² B、a³·a²＝a⁵ C、(a⁴)²＝a⁶ D、a³＋a⁴＝a⁷

查看试题解析
2. 新冠病毒（2019－nCoV）是一种新型病毒，它的直径约60～220nm，平均直径为100nm（纳米）.1纳米＝10^－9米，那么100nm用科学记数法可以表示为（）

A、0.1×10^-6米 B、10×10^-7 米 C、1×10^-6 米 D、1×10^-7米

查看试题解析
3. 下列哪组长度的三条线段能组成三角形?（）

A、1cm、2cm、4cm B、3cm、4cm、7cm C、2cm、2cm、1cm D、5cm、3cm、2cm

查看试题解析
4. 如图，AB∥DE，BC∥EF，则∠E与∠B的关系一定成立的是（）

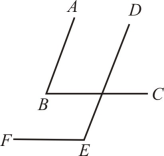A、互余 B、∠E=2∠B C、相等 D、互补

查看试题解析
5. 如图，若要使AD∥BC，则可以添加条件（）

A、∠2＝∠3 B、∠B＋∠BCD＝180° C、∠1＝∠4 D、∠1＝∠3

查看试题解析
6. 下列各式从左边到右边的变形，是因式分解且分解正确的是（）

A、（a＋1）（a－1）＝a²－1 B、a²－8a＋16＝（a－4）² C、a²－2a+4＝（a－2）² D、ab＋ac＋1＝a（b＋c）＋1

查看试题解析
7. 用一个容量为2GB（1GB=2¹⁰MB）的便携式优盘存储数码照片，若每张数码照片的文件大小都为16MB，则理论上可以存储的照片数是（）

A、2¹⁰张 B、2⁸张 C、2⁷张 D、2⁶张

查看试题解析
8. 下列各式能用平方差公式计算的是（）

A、（－2x+y）（－2x－y） B、（2x+y）（x－2y） C、（x－2y）（－x+2y） D、（－2x+y）（－x+2y）

查看试题解析
9. 我国古代数学名著《张邱建算经》中记载：“今有清酒一斗直粟十斗，醑酒一斗直粟三斗.今持粟三斛，得酒五斗，问清、醑酒各几何？”意思是：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子.现在拿30斗谷子，共换了5斗酒，问清、醑酒各几斗？如果设清酒x斗，醑酒y斗，那么可列方程组为（）

A、 ${\begin{array}{l} x + y = 5 ， \\ 10 x + 3 y = 30 \end{array}$ B、 ${\begin{array}{l} x + y = 5 ， \\ 3 x + 10 y = 30 \end{array}$ C、 ${\begin{array}{l} x + y = 5 ， \\ \frac{x}{10} + \frac{y}{3} = 30 \end{array}$ D、 ${\begin{array}{l} x + y = 5 ， \\ \frac{x}{3} + \frac{y}{10} = 30 \end{array}$

查看试题解析
10. 对于a、b两数定义@的一种运算：a@b=（a▪b）a⁺b（其中等式右边的▪和+是通常意义下的乘法与加法），则下列结论：
①若a=1，b=－2，则a@b=－ $\frac{1}{2}$ ； ②若（－1）@x=1，则x=1；③a@b=b@a；④当a、b互为相反数时，a@b的值总是等于1.其中正确的是（）

A、①②④ B、①③ C、①③④ D、②③

查看试题解析

二、填空题

11. 正五边形的内角和等于度.

查看试题解析
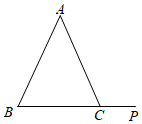
12. 如图，已知∠ACP＝115°，∠B＝65°，则∠A＝.

查看试题解析
13. 若 ${\begin{array}{l} x = 4 \\ y = 1 \end{array}$ 是二元一次方程2x＋3y＝k的一个解，则k的值是.

查看试题解析
14. 多项式 $4 x^{3} y^{2} + 8 x^{2} y^{3} - 2 x^{2} y$ 分解因式时所提取的公因式是.

查看试题解析
15. 如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C平移的距离CC＇＝.

查看试题解析
16. 若a^m＝9，aⁿ＝3，则a^m-n＝.

查看试题解析
17. 已知关于x的代数式4x²+ax+9是完全平方式，则a=.

查看试题解析
18. 如图，将三角形纸片ABC沿EF折叠，使得A点落在BC上点D处，连接DE，DF， $∠ C E D = ∠ C D E = 45 °$ .设 $∠ B D F = α$ ， $∠ B F D = β$ ，则α与β之间的数量关系是.

查看试题解析

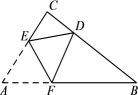
三、解答题

19. 计算或化简：

(1)、 $2^{0} + (- 2)^{2} - (\frac{1}{3})^{- 1}$

(2)、a² $\cdot$ a⁴＋a⁸÷a²+（－2a²）³

(3)、（a+1）²+a（3－a）；

(4)、（m+1）² $\cdot$ （m﹣1）².

查看试题解析
20. 因式分解：

(1)、mx²﹣my²；

(2)、2x²－8x+8.

查看试题解析
21. 先化简，再求值：（x－2）²＋4（x－y）－（2y－1）² ，其中x＝4.85，y＝2.575.

查看试题解析
22. 如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点.仅用无刻度的直尺完成下列作图.

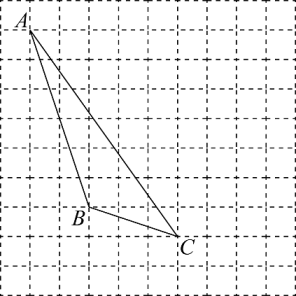(1)、画出△ABC向右平移4个单位后的图形△A₁B₁C₁（注意标上字母）；

(2)、画出△ABC的中线CD（注意标上字母）；

(3)、画出满足△QBC与△ABC面积相等的一个格点Q（与点A不重合）.

查看试题解析
23. 如图，△ABC中，D为AC边上一点，过D作DE∥AB，交BC于E；F为AB边上一点，连接DF并延长，交CB的延长线于G，且∠DFA＝∠A.

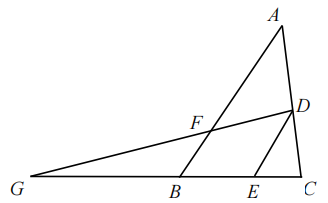(1)、求证：DE平分∠CDF；

(2)、若∠C＝80°，∠ABC＝60°，求∠G的度数.

查看试题解析
24. 阅读以下材料：
若x²－4x＋y²－10y＋29=0，求x、y的值.
思路分析：一个方程求两个未知数显然不容易，考虑已知等式的特点，将其整理为两个完全平方式的和，利用其非负性转化成两个一元一次方程，进而求出x、y.
解：∵x²－4x＋y²－10y＋29=0，
∴（x²－4x+4）＋（y²－10y＋25）=0，
∴（x－2）²+（y－5）²=0，
∴x=2，y=5.
请你根据上述阅读材料解决下列问题：

(1)、若m²＋2m＋n²－6n＋10＝0，则m+n= ；

(2)、请你说明：无论x、y取何值，代数式x²－4xy＋5y²＋2y＋5的值一定是正数.

查看试题解析
25. 数形结合是解决数学问题的一种重要思想方法，借助图形的直观性，可以帮助理解数学问题.

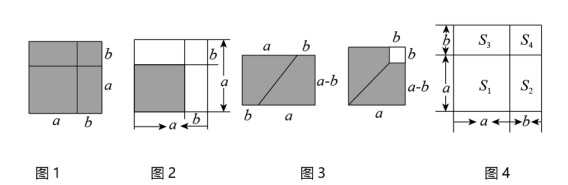(1)、请写出图1，图2，图3阴影部分的面积分别能解释的数学公式.

图1：；图2：；图3：.

(2)、其中，完全平方公式可以从“数”和“形”两个角度进行探究，并通过公式的变形或图形的转化可以解决很多数学问题.

例如：如图4，已知a+b＝3，ab＝1，求a²+b²的值.

方法一：从“数”的角度

解：∵a+b＝3，

∴（a+b）²＝9，即：a²+2ab+b²＝9，

又∵ab＝1

∴a²+b²＝7.

方法二：从“形”的角度

解：∵a+b＝3，

∴S_大正方形=9，

又∵ab＝1，

∴S₂＝S₃＝ab＝1，

∴S₁+S₄＝S_大正方形﹣S₂﹣S₃＝9﹣1﹣1＝7.即a²+b²＝7.
若（5﹣x）▪（x﹣1）＝3，则（5﹣x）²+（x﹣1）²＝；

(3)、如图，点C是线段AB上的一点，以AC，BC为边向两边作正方形，设AB＝10，两正方形的面积和S₁+S₂＝72，求图中阴影部分面积.

查看试题解析
26. 引入概念1：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”.
引入概念2：从不等边三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形.若分成的两个小三角形中一个是满足有两个角相等的三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”.

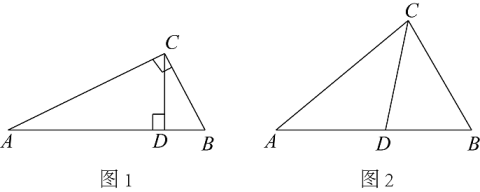(1)、如图1，在Rt△ABC中，∠ACB=90°，CD⊥AB，请写出图中两对“等角三角形”.
①；②.

(2)、如图2，在△ABC中，CD为角平分线，∠A=40°，∠B=60°.请你说明CD是△ABC的等角分割线.

(3)、在△ABC中，若∠A=40°，CD为△ABC的等角分割线，请你直接写出所有可能的∠B度数.

查看试题解析