江苏省无锡市滨湖区2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-07-14 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列长度的三条线段首尾顺次相接能组成三角形是（  ）
    A、1，2，3 B、2，4，7 C、3，4，8 D、2，3，4

    查看试题解析

  • 2. 下列运算正确的是（       ）
    A、（a2）3＝a6 B、a•a3＝a3 C、a2＋a2＝a4 D、a6÷a2＝a3

    查看试题解析

  • 3. 若（x﹣2）（x+3）=x2+ax+b，则a，b的值分别为（   ）
    A、a=5，b=﹣6 B、a=5，b=6 C、a=1，b=6 D、a=1，b=﹣6

    查看试题解析

  • 4. 若△ABC三个角的大小满足条件∠A：∠B：∠C＝1：3：4，则∠C的大小为（  ）
    A、22.5° B、45° C、67.5° D、90°

    查看试题解析

  • 5. 如图，AD、BE、CF是△ABC三边的中线，若S△ABC=12，则图中的阴影部分的面积是（  ）

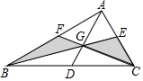    A、3 B、4 C、5 D、6

    查看试题解析

  • 6. 如图，直线AB∥CD，∠M=90° ， ∠MPA＝32°，则∠MEC的度数是（ ）

    A、58° B、122° C、132° D、148°

    查看试题解析

  • 7. 如图，AF是∠BAC的平分线， DF∥AC，若∠1＝25°，则∠BDF的度数为（　　）

    A、25° B、50° C、75° D、100°

    查看试题解析

  • 8. 已知多项式x2−2(m+1)x+1是完全平方式，则m的值为（  ）
    A、2或0 B、-2 C、0 D、-2或0

    查看试题解析

  • 9. 已知10a=6，10b=2，10c=72，用含有a和b的代数式表示c为（  ）
    A、c=a+b B、c=2a+b C、c=2a+2b D、c=2a+3b

    查看试题解析

  • 10. 已知2x2+2y2=2x-6y-5，则x+y的值是（  ）
    A、-1 B、-2 C、1 D、2

    查看试题解析

二、填空题

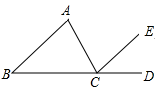
  • 11. 计算：a2•a3= ．

    查看试题解析

  • 12. “燕雪花大轩台是诗仙李白眼里的雪花，单个雪花的重量其实很轻，只有0.00003kg左右，0.00003用科学记数法可表示为.

    查看试题解析

  • 13. 如图所示，请添加一个条件，使AB//CE.则添加的条件为.

    查看试题解析

  • 14. 已知xm=6，xn=4，则x2m-n的值为.

    查看试题解析

  • 15. 有下列运算：①2a2b⋅3ab2=6a3b3；②（-2a）2=-4a2；③（a+2b）（a-2b）=a2-2b2；④（a+2）2=a2+4；⑤（-a3）2-（a2）3=0，其中正确的有.（填写相应的序号）

    查看试题解析

  • 16. 已知一个多边形的每一个内角都比与它相邻的外角的4倍多30°，这个多边形的边数为 ， 这个多边形共有条对角线.

    查看试题解析

  • 17. 如图，在RtΔABC中，∠ACB=90°，点D、E分别在AB、AC上，连接DE，将ΔADE沿DE翻折，使点A的对应点F落在BC的延长线上，若FD平分∠EFB，∠AEF=160°，则∠B的度数为.

    查看试题解析

  • 18. 如图，在正方形ABCD中，AB=6cm，E是AD边上的中点，动点P从A出发，以1cm/s的速度沿着A-B-C-D-E运动，终点到达点E，当点P运动s时，ΔBPE的面积为12cm2

    查看试题解析

三、解答题

  • 19. 计算：
    (1)、20220+（12）-2-（-2）2；
    (2)、3m3⋅m2-（2m4）2÷m3；
    (3)、（2x-3）（x+1）-x（x+4）；
    (4)、（2a+b+3）（2a-b+3）-（2a+3）2.

    查看试题解析

  • 20. 先化简，再求值：2（x+1）2-3（x-1）（x+1）+x（x-3），其中x=-1.

    查看试题解析

  • 21. 规定a*b＝3a×3b ， 求：
    (1)、求1*2；
    (2)、若2*（x+1）＝81，求x的值.

    查看试题解析

  • 22. 如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点.△ABC的顶点都在方格纸格点上.

    (1)、请在图中画出ABC先向上平移3个单位，再向左平移2个单位后的△A1B1C1；
    (2)、图中AC与A1C1的关系是；
    (3)、图中△ABC的面积是；
    (4)、请利用三角尺，画出△A1B1C1边B1C1上的高A1D，垂足为点D.

    查看试题解析

  • 23. 如图，在△ABC中，AD为边BC上的高，点E为边BC上的一点，连接AE.

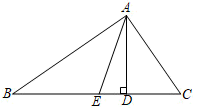    (1)、当AE为边BC上的中线时，若AD=6，△ABC的面积为24，求CE的长；
    (2)、当AE为∠BAC的角平分线时，若∠C=66°，∠B=36°，求∠DAE的度数.

    查看试题解析

  • 24. 如图1，已知直线AB//CD，∠A=∠C=100°.

    (1)、试判断直线AD和BC的位置关系?并说明理由；
    (2)、如图2若E、F在CD上，且满足∠DBF=∠ABD，BE平分∠CBF，是否存在∠BEC=∠ADB?如果存在，请求出∠ADB的度数，如果不存在，请说明理由.

    查看试题解析

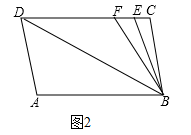  • 25. 我们知道，图形是一种重要的数学语言，它直观形象，能有效地表示一些代数中的数量关系，而运用代数思想也能巧妙的解决一些图形问题.比如：用图1所示的正方形与长方形纸片可以拼成一个图2所示的正方形.

    请你解决下列问题：

    (1)、问题发现：利用不同的代数式表示图2中影部分的面积S，写出你从中获得的等式为；
    (2)、类比探究：已知x满足（22-x）（x-18）=2，

    则（22-x）2+（x一18）2=；

    (3)、拓展延伸：如图3，正方形ABCD和正方形EFGH重叠，其重叠部分是一个长方形，分别延长HE、FE，交AB和AD于P、Q两点，构成的四边形BMEP和四边形QEND都是正方形，四边形APEQ是长方形.若MF=10，NH=30，长方形EMCN的面积为200.求正方形ABCD的面积.

    查看试题解析

  • 26. 【概念认识】

    如图①，在∠ABC中，若∠ABD=∠DBE=∠EBC，则BD，BE叫做∠ABC的“三分线”.其中，BD是“邻BA三分线”，BE是“邻BC三分线”.

    (1)、如图②，在△ABC中，∠A=50°，∠ABC=60°，若∠ABC的邻BA三分线BD交AC于点D，则∠BDC的度数为；

    (2)、如图③，在△ABC中，BP，CP分别是∠ABC邻BA三分线和∠ACB邻CA三分线，且∠BPC=80°，求∠A的度数；

    (3)、【延伸推广】
    在ΔABC中，∠ABC=45° ， ∠ACD是ΔABC的外角，∠ABC的邻BC三分线所在的直线与∠ACD的三分线所在的直线交于点P.当∠A比∠P大20°时，求∠P的度数.

    查看试题解析