江苏省泰州市海陵区五校2021-2022学年七年级下学期期中考试数学试卷

试卷更新日期：2022-07-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、a²•a³＝a⁶ B、（a²）³＝a⁵ C、a²＋a²＝a⁴ D、2a²﹣a²＝a²

查看试题解析
2. 下面各组线段中，能组成三角形的是（）

A、2，3，4 B、4，4，8 C、5，4，10 D、6，7，14

查看试题解析
3. 下列多项式乘法中，不能用平方差公式计算的是（）。

A、（﹣x﹣y）（x﹣y） B、（﹣x+y）（x﹣y） C、（﹣x﹣y）（﹣x+y） D、（x+y）（﹣x+y）

查看试题解析
4. 若（a﹣1）x^|a^|^﹣¹＋3y＝1是关于x、y的二元一次方程，则a＝（）

A、1 B、2 C、﹣2 D、2和﹣2

查看试题解析
5. 如图，直线AB∥CD，∠A=115°，∠E=80°，则∠CDE的度数为（　　）

A、 $15^{\circ}$ B、 $20^{\circ}$ C、 $25^{\circ}$ D、 $30^{\circ}$

查看试题解析
6. 如图是正方形卡片A类、B类和长方形卡片C类.现有A类卡片4张，B类卡片1张，C类卡片4张，则这9张卡片能拼成的正方形的边长为（）

A、a+2b B、2a+b C、2a+2b D、a+b

查看试题解析

二、填空题

7. 计算： ${(- 3 x y^{2})}^{3} =$ .

查看试题解析
8. 如图，折叠宽度相等的长方形纸条，若 $∠ 2 = 48^{\circ}$ ，则 $∠ 1 =$ .

查看试题解析
9. 一个三角形的两边长分别为 2 和 5，若第三边取奇数，则此三角形的周长为.

查看试题解析
10. 新型冠状病毒属于冠状病毒科，病毒粒子呈球形，直径为0.00000012m，用科学记数法表示m.

查看试题解析
11. 计算 $(x + a) (2 x - 1)$ 的结果中不含关于字母x的一次项，则a=.

查看试题解析
12. 小亮解方程组 ${\begin{array}{l} 2 x + y = 0 \\ 2 x - y = ● \end{array}$ 的解为 ${\begin{array}{l} x = 5 \\ y = ★ \end{array}$ ，由于不小心，滴上了两滴墨水，刚好遮住了两个数●和★，请你帮他找回★和●，这个数★＝， ●＝.

查看试题解析
13. 已知， $1 5^{a} = 25$ 和 $1 5^{b} = 9$ ， $a = - b - c$ ，则 $1 5^{c} =$ .

查看试题解析
14. 已知在 $Δ A B C$ 中，已知点 $D$ 、 $E$ 、 $F$ 分别为 $B C$ 、 $A D$ 、 $C E$ 的中点，且 $S_{Δ B E F} = 4 c m^{2}$ ，则 $S_{Δ A B C}$ 的值为 $c m^{2}$ .

查看试题解析
15. 如图，∠A＝70°，O是AB上一点，直线OD与AB所夹的∠AOD＝100°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转.

查看试题解析
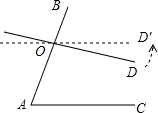16. 已知关于x，y的方程组 ${\begin{array}{l} x + 2 y = 1 - a \\ x - y = 2 a - 5 \end{array}$ 若 $x^{y}$ =1，则a=.

查看试题解析

三、解答题

17. 计算：

(1)、 ${(\frac{1}{2})}^{- 1} + {(π - 2020)}^{0} - {(- 5)}^{2}$

(2)、 ${(- 0.25)}^{2020} \times 4^{2021}$

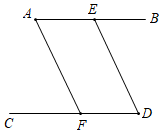
查看试题解析
18. 计算：

(1)、2a（a-2a²）

(2)、（x-2y-1）（x+2y-1）

查看试题解析
19. 分解因式：

(1)、2x²﹣4xy+2y²

(2)、m²（m﹣n）+（n﹣m）

查看试题解析
20. 已知：如图，AB∥CD，∠A=∠D
求证：AF∥ED

请你将证明过程补充完整

证明：∵AB∥CD，

∴   = （   ），

∵∠A=∠D，

∴ = （   ），

∴AF∥ED（   ）.

查看试题解析
21. 解方程组

(1)、 ${\begin{array}{l} x + y = - 2 \\ x + 2 y = 4 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{x + 1}{5} = \frac{y - 3}{2} \\ 3 x + 4 y = 32 \end{array}$ .

查看试题解析
22. 先化简，再求值： ${(5 a - 3 b)}^{2} - 2 (5 a + 3 b) (4 a - 3 b)$ ，其中a=2，b=-1.

查看试题解析
23. 如图，已知CD平分∠ACB，∠1＝∠2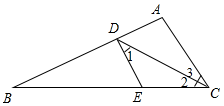

(1)、求证：DE∥AC；

(2)、若∠3＝30°，∠B＝25°，求∠BDE的度数.

查看试题解析
24. 若方程组 ${\begin{cases} 2 x - y = 7 \\ a x + y = b \end{cases}$ 和方程组 ${\begin{cases} x + b y = a \\ 3 x + y = 8 \end{cases}$ 有相同的解，求a，b的值.

查看试题解析
25. 若x，y满足x²+y²＝8，xy＝2，求下列各式的值.

(1)、（x+y）²；

(2)、x⁴+y⁴；

(3)、x﹣y.

查看试题解析
26. 阅读材料；若m²﹣2mn+2n²﹣8n+16＝0，求m、n的值.
解：∵m²﹣2mn+2n²﹣8n+16＝0
∴（m²﹣2mn+n²）+（n²﹣8n+16）＝0，
∴（m﹣n）²+（n﹣4）²＝0，
∴（m﹣n）²＝0，（n﹣4）²＝0，
∴m＝4，n＝4.
根据你的观察，探究下面的问题：

(1)、已知x²+2xy+2y²+2y+1＝0.则2x+3y的值为；

(2)、已知△ABC的边长a、b、c是三个互不相等的正整数，且满足a²+b²﹣4a﹣6b+13＝0，求c的值；（写出求解过程）

(3)、已知a﹣b＝10，ab+c²﹣16c+89＝0，则a+b+c的值为.

查看试题解析
27. 已知 $△$ ABC，P 是平面内任意一点（A、B、C、P 中任意三点都不在同一直线上）.连接 PB、PC，设∠PBA＝s°，∠PCA＝t°，∠BPC＝x°，∠BAC＝y°.

(1)、如图，当点 P 在 $△$ ABC 内时，
①若 y＝70，s＝10，t＝20，则 x＝ ▲ ；
②探究 s、t、x、y 之间的数量关系，并证明你得到的结论.

(2)、当点 P 在 $△$ ABC 外时，直接写出 s、t、x、y 之间所有可能的数量关系，并画出相应的图形.

查看试题解析