江苏省苏州市2021-2022学年七年级下学期期中数学试卷
试卷更新日期:2022-07-14 类型:期中考试
一、单选题
-
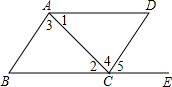
1. 下列各式从左到右的变形,是因式分解的是( )A、ab+bc+d=a(b+c)+d B、(a+2)(a-2)=a2-4 C、a3-1=(a-1)(a2+a+1) D、6ab2=2ab•3b2. 如图,不能判定AB∥CD的条件是( )
 A、∠1=∠2 B、∠B+∠BCD=180° C、∠3=∠4 D、∠B=∠53. 已知a=(-0.3)0 , b=-3-1 , c= ,比较a,b,c的大小( )A、a<b<c B、b<c<a C、a<c<b D、b<a<c4. 若M=(x-2)(x-7),N=(x-6)(x-3),则M与N的关系为( )A、M=N B、M>N C、M<N D、M与N的大小由x的取值而定5. (-8)2022+(-8)2021能被下列数整除的是( )A、3 B、5 C、7 D、96. 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C,在△ABC中,∠DBA+∠DCA=40°,则∠A的度数是( )
A、∠1=∠2 B、∠B+∠BCD=180° C、∠3=∠4 D、∠B=∠53. 已知a=(-0.3)0 , b=-3-1 , c= ,比较a,b,c的大小( )A、a<b<c B、b<c<a C、a<c<b D、b<a<c4. 若M=(x-2)(x-7),N=(x-6)(x-3),则M与N的关系为( )A、M=N B、M>N C、M<N D、M与N的大小由x的取值而定5. (-8)2022+(-8)2021能被下列数整除的是( )A、3 B、5 C、7 D、96. 有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C,在△ABC中,∠DBA+∠DCA=40°,则∠A的度数是( )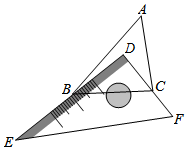 A、40° B、45° C、50° D、55°7. 如图,正方形卡片A类,B类和长方形卡片C类若干张,要拼一个长为(a+mb),宽为(3a+b)的大长方形(m为常数),若知道需用到的B类卡片比A类卡片少1张,则共需C类卡片( )张.
A、40° B、45° C、50° D、55°7. 如图,正方形卡片A类,B类和长方形卡片C类若干张,要拼一个长为(a+mb),宽为(3a+b)的大长方形(m为常数),若知道需用到的B类卡片比A类卡片少1张,则共需C类卡片( )张.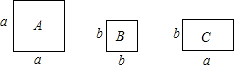 A、5 B、6 C、7 D、88. 将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2的度数等于( )
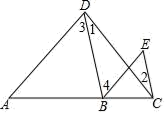
A、5 B、6 C、7 D、88. 将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2的度数等于( )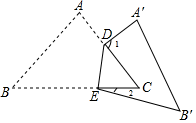 A、10° B、15° C、20° D、25°
A、10° B、15° C、20° D、25°二、填空题
-
9. 熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播.经测量,医用外科口罩的熔喷布厚度约为0.000156米,将0.000156用科学记数法表示应为.10. 已知一个多边形的每个内角都相等,其内角和为2340°,则这个多边形每个外角的度数是°.11. 若2023x=5,2023y =4,则20232x-y的值为.12. 小兰在计算一个二项式的平方时,得到的正确结果是x2+(■-1)xy+9y2 , 但中间项的某一部分不慎被墨汁污染了,则■处所对应的数可能是.13. 如图,海关大厦与电视台大厦的大楼顶部各有一个射灯,当光柱相交时,且它们都在同一个平面内,若∠1=76°,则∠2+∠3= °.
 14. 如图,.
14. 如图,. 15. 定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a、b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
15. 定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a、b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.例如:(4+i)+(6﹣2i)=(4+6)+(1﹣2)i=10﹣i;
(2﹣i)(3+i)=6﹣3i+2i﹣i2=6﹣i﹣(﹣1)=7﹣i;
(2+i)2=4+4i+i2=4+4i﹣1=3+4i.
根据以上信息,完成下面计算:(2+i)(1﹣2i)+(2﹣i)2=.
16. 如图,在四边形ABCD中,∠A+∠B=210°,作∠ADC、∠BCD的平分线交于点O1 , 再作∠O1DC、∠O1CD的平分线交于点O2 , 则∠O2的度数为.
三、解答题
-
17. 计算(1)、x5•(-2x)3+x9÷x2•x-(3x4)2(2)、(2a-3b)2-4a(a-2b)(3)、(3x-y)2(3x+y)2(4)、(2a-b+5)(2a+b-5)18. 因式分解(1)、2a2b-8ab2+8b3(2)、4a2(m-n)+9(n-m)(3)、81x4-16(4)、(m2+5)2-12(m2+5)+3619. 已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
 20. 已知x+y=3,xy= , 求下列各式的值:(1)、(x2-2)(y2-2);(2)、x2y-xy2.21. 解决下列问题:(1)、若4a-3b+7=0,求32×92a+1÷27b的值;(2)、已知x满足22x+4-22x+2=96,求x的值.(3)、对于任意有理数A,B,C,D,我们规定符号(a,b)⋇(c,d)=ad-bc+2,例如:(1,3)⋇(2,4)=1×4-2×3+2=0.当a2+a+5=0时,求(2a+1,a-2)⋇(3a+2,a-3)的值.22. 阅读材料:已知a+b=8,ab=15,求a2+b2的值.
20. 已知x+y=3,xy= , 求下列各式的值:(1)、(x2-2)(y2-2);(2)、x2y-xy2.21. 解决下列问题:(1)、若4a-3b+7=0,求32×92a+1÷27b的值;(2)、已知x满足22x+4-22x+2=96,求x的值.(3)、对于任意有理数A,B,C,D,我们规定符号(a,b)⋇(c,d)=ad-bc+2,例如:(1,3)⋇(2,4)=1×4-2×3+2=0.当a2+a+5=0时,求(2a+1,a-2)⋇(3a+2,a-3)的值.22. 阅读材料:已知a+b=8,ab=15,求a2+b2的值.解:a2+b2=(a+b)2-2ab=64-30=34.
参考上面的方法求解下列问题:
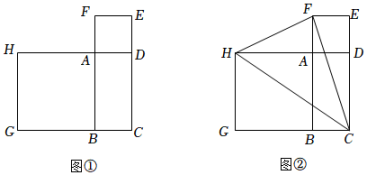 (1)、已知x满足(x-2)(3-x)=-1,求(x-2)2+(3-x)2的值.(2)、如图①,已知长方形ABCD的周长为12,分别以AD、AB为边,向外作正方形ADEF、ABGH,且正方形ADEF、ABGH的面积和为20.
(1)、已知x满足(x-2)(3-x)=-1,求(x-2)2+(3-x)2的值.(2)、如图①,已知长方形ABCD的周长为12,分别以AD、AB为边,向外作正方形ADEF、ABGH,且正方形ADEF、ABGH的面积和为20.① 求长方形ABCD的面积;
②如图②,连接HF、CF、CH,求△CFH的面积.
23. 利用我们学过的完全平方公式与不等式知识能解决方程或代数式的一些问题,阅读下列两则材料:材料一:已知m2-2mn+2n2-8n+16=0,求m、n的值.
解:∵m2-2mn+2n2-8n+16=0,
∴(m2-2mn+n2)+(n2-8n+16)=0,
∴(m-n)2+(n-4)2=0,
∵(m-n)2≥0,(n-4)2≥0
∴(m-n)2=0,(n-4)2=0
∴m=n=4.
材料二:探索代数式x2+4x+2与-x2+2x+3是否存在最大值或最小值?
①x2+4x+2=(x2+4x+4)-2=(x+2)2-2,∵(x+2)2≥0,∴x2+4x+2=(x+2)2-2≥-2.
∴代数式x2+4x+2有最小值-2;
②-x2+2x+3=-(x2-2x+1)+4=-(x-1)2+4,∵-(x-1)2≤0,∴-x2+2x+3=-(x-1)2+4≤4.
∴代数式-x2+2x+3有最大值4.
学习方法并完成下列问题:
(1)、代数式x2-6x+3的最小值为;(2)、如图,在紧靠围墙的空地上,利用围墙及一段长为100米的木栅栏围成一个长方形花圃,为了设计一个尽可能大的花圃,设长方形垂直于围墙的一边长度为x米,则花圃的最大面积是多少?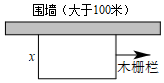 (3)、已知△ABC的三条边的长度分别为a,b,c,且a2+b2+74=10a+14b,且c为正整数,求△ABC周长的最小值.24. 【生活常识】
(3)、已知△ABC的三条边的长度分别为a,b,c,且a2+b2+74=10a+14b,且c为正整数,求△ABC周长的最小值.24. 【生活常识】射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图1,MN是平面镜,若入射光线AO与水平镜面夹角为∠1,反射光线OB与水平镜面夹角为∠2,则∠1=∠2.
【应用探究】
有两块平面镜OM,ON,入射光线AB经过两次反射,得到反射光线CD.
 (1)、如图2,若OM⊥ON,试证明AB∥CD;(2)、如图3,光线AB与CD相交于点P,若∠MON=48°,求∠BPC的度数;(3)、如图4,光线AB与CD所在的直线相交于点P,∠MON=α,∠BPC=β,试猜想α与β之间满足的数量关系,并说明理由.
(1)、如图2,若OM⊥ON,试证明AB∥CD;(2)、如图3,光线AB与CD相交于点P,若∠MON=48°,求∠BPC的度数;(3)、如图4,光线AB与CD所在的直线相交于点P,∠MON=α,∠BPC=β,试猜想α与β之间满足的数量关系,并说明理由.