河南省信阳市潢川县2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-07-14 类型：期中考试

进入出卷网下载

一、单选题

1. 公元前6世纪，古希腊的毕达哥拉斯学派有一种观点﹣“万物皆数”，即一切量都可以用整数或整数的比（分数）表示.后来这一学派中的希帕索斯发现，边长为1的正方形对角线的长度不能用整数或整数的比表示，这令毕达哥拉斯学派感到惊恐不安，由此引发了第一次数学危机.这类“不能用整数或整数的比表示的数”指的是（）

A、有理数 B、无理数 C、零 D、负数

查看试题解析
2. 如图，在平面直角坐标系中，被手盖住的点的坐标可能为（）

A、(4，5) B、(﹣4，5) C、(﹣4，﹣5) D、(4，﹣5)

查看试题解析
3. 如图，已知 $∠ 1 = 55 °$ ， $∠ 2 = 135 °$ ，则下列说法错误的是（）

A、 $∠ 4 = 135 °$ B、∠2与∠3互为邻补角 C、a与b相交 D、∠1与∠2是内错角

查看试题解析
4. 下列选项中错误的是（）

A、 $\sqrt{- 2}$ 没意义 B、 $\sqrt{2}$ 是2的平方根 C、 $\sqrt[3]{- 2}$ 是负数 D、 $\sqrt{2} < \sqrt[3]{2}$

查看试题解析
5. 如图，快艇从P处向正北方向航行到A处时，向左转 $40 °$ 航行到B处，再向右转 $60 °$ 继续航行，此时快艇航行的方向为（）

A、北偏东 $60 °$ B、北偏西 $60 °$ C、北偏东 $20 °$ D、北偏西 $20 °$

查看试题解析
6. 如图，下列推理错误的是（）

A、∵ $∠ 1 = ∠ 2$ ， ∴a $∥$ b B、∵b $∥$ c，∴ $∠ 3 + ∠ 4 = 180 °$ C、∵a $∥$ b，b $∥$ c，∴a $∥$ c D、∵ $∠ 1 = ∠ 4$ ， ∴a $∥$ c

查看试题解析
7. 如图，四边形 $A B C D$ 中，BC $∥$ AD， $C A$ 平分 $∠ B C D$ ， $∠ 1 = 35 °$ ， ∠D的度数是（）

A、110° B、120° C、130° D、70°

查看试题解析
8. 下列命题中，真命题的个数有（）.
①无限小数是无理数；
②立方根等于它本身的数有两个，是0和1；
③同位角相等；
④过一点有且只有-条直线与已知直线平行

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 如图在正方形网格中，若 $A (10 ， 10)$ ， $B (20 ， 0)$ ，则C点的坐标为（）

A、 $(- 30 ， - 20)$ B、 $(30 ， - 20)$ C、 $(- 20 ， - 30)$ D、 $(20 ， - 30)$

查看试题解析
10. 已知 $\sqrt[3]{0.214} \approx 0.5981$ ， $\sqrt[3]{2.14} \approx 1.289$ ， $\sqrt[3]{21.4} \approx 2.776$ ，则 $\sqrt[3]{21400} \approx$ （）

A、 $27.76$ B、 $12.89$ C、 $59.81$ D、 $5.981$

查看试题解析

二、填空题

11. 正数m的一个平方根是 $2 a - 1$ ，它的另一个平方根是.

查看试题解析
12. 在实数 $\frac{1}{3}$ 、0、-2、 $- \sqrt{3}$ 中，最小的数是.

查看试题解析
13. 如图， $A E$ 平分 $∠ B A C$ ， $C E$ 平分 $∠ A C D$ ，要使 $A B / / C D$ ，则 $∠ 1$ 和 $∠ 2$ 应满足的条件是.

查看试题解析
14. 在平面直角坐标系中，若点M（1，3）与点N（x ， 3）之间的距离是5，则x的值是．

查看试题解析
15. 将正整数的算术平方根按如图所示的规律排列下去.若用有序实数对 $(m ， n)$ 表示第m排，从左到右第n个数，如 $(4 ， 2)$ 表示实数 $\sqrt{8}$ ，则这些实数中从小到大第十个有理数对应的有序数对是.

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{100} + \sqrt[3]{- 27} - 2 \times \sqrt{\frac{1}{4}}$

(2)、 $\sqrt{(- 3)^{2}} + \sqrt{6} + | \sqrt{6} - 3 |$

查看试题解析
17. 已知2x是36的平方根， $(y - 4)^{3} + 8 = 0$ ，求x，y的值.

查看试题解析
18. 如图，已知 $∠ A = ∠ C$ ， EF $∥$ DB.说明 $∠ A E F = ∠ D$ 的理由.

解：因为 $∠ A = ∠ C$ （已知），

所以 $A B$ $∥$   （   ）.

所以 $∠ D = ∠ B$ （   ）.

又因为EF $∥$ DB（已知），

所以 $∠ B =$ （   ）.

所以 $∠ A E F = ∠ D$ .（   ）.

查看试题解析
19. 如图，直线AB、CD相交于点O，OM⊥AB.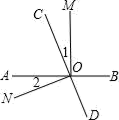

(1)、若∠1=∠2，证明：ON⊥CD；

(2)、若∠1= $\frac{1}{4}$ ∠BOC，求∠BOD的度数.

查看试题解析
20. 如图，在三角形 $A B O$ 中， $O A ⊥ A B$ ，垂足为A，过点A画 $O B$ 的垂线段 $A C$ ，垂足为点C，过点C画直线CD $∥$ OA，交线段 $A B$ 于点D.

(1)、补全图形（按要求画图）；

(2)、求 $∠ C D B$ 的度数：

(3)、如果 $O A = 4$ ， $A B = 3$ ， $O B = 5$ ，求点A到直线 $O B$ 的距离.

查看试题解析
21. 如图，用两个边长为 $\sqrt{18} c m$ 的小方形纸片拼成一个大的正方形纸片，沿着大正方形纸片的边的方向截出一个长方形纸片，能否使截得的长方形纸片的长是宽的2倍，且面积为 $30 c m^{2}$ ？请说明理由.

查看试题解析
22. 如图，在平面直角坐标系中，同时将点 $A (- 1 ， 0)$ 、 $B (3 ， 0)$ 向上平移2个单位长度再向右平移1个单位长度，分别得到A、B的对应点C、D.连接 $A C$ ， $B D$ ， $C D$ .

(1)、求点C、D的坐标，并描出A，B，C，D点，求四边形 $A B D C$ 面积；

(2)、在x坐标轴上是否存在点P；连接 $P A$ 、 $P C$ 使 $S_{△ P A C} = S_{四边形 A B D C}$ ？若存在，求点P坐标；若不存在，请说明理由.

查看试题解析
23. 已知整点（横纵坐标都是整数） $P_{0}$ 在平面直角坐标系内做“跳马运动”（也就是中国象棋式“日字”型跳跃）.例如，在下图中，从点A做一次“跳马运动”可以到点B，但是到不了点C.
设 $P_{0}$ 做一次跳马运动到点 $P_{1}$ ，再做一次跳马运动到点 $P_{2}$ ，再做一次跳马运动到点 $P_{3}$ ， ……，如此继续下去

(1)、若 $P (1 ， 0)$ ，则 $P_{1}$ 可能是下列哪些点；
$D (- 1 ， 2)$ ； $E (- 1 ， - 1)$ ； $F (- 2 ， 0)$ ；

(2)、已知点 $P_{0} (4 ， 2)$ ， $P_{2} (1 ， 3)$ ，则点 $P_{1}$ 的坐标为；

(3)、 $P_{0}$ 为平面上一个定点，则点 $P_{3}$ 、 $P_{9}$ 、 $P_{16}$ 可能与 $P_{0}$ 重合的是；

(4)、 $P_{0}$ 为平面上一个定点，则线段 $P_{0} P_{7}$ 长的最小值是.

查看试题解析