3.8函数的零点问题——2023年高考数学一轮复习（新高考地区专用）

试卷更新日期：2022-07-14 类型：一轮复习

进入出卷网下载

一、单选题

1. 已知函数 $f (x) = c o s 2 x + c o s x$ ，且 $x \in [0 ， 2 π]$ ，则 $f (x)$ 的零点个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 已知函数 $f (x) = {\begin{array}{l} x ， x \geq 0 \\ - x^{2} ， x < 0 \end{array}$ ，若方程 $f (x) = a e^{x}$ 有两个不相等的实数根，则实数 $a$ 的取值范围为（）

A、 $(\frac{1}{e} ， + \infty)$ B、 $(0 ， \frac{1}{e})$ C、 $(- \infty ， - \frac{1}{e})$ D、 $(- \frac{1}{e} ， 0)$

查看试题解析
3. 已知函数 $f (x)$ 为定义在 $R$ 上的单调函数，且 $f (f (x) - 2^{x} - 2 x) = 10$ ．若函数 $g (x) = {\begin{array}{l} f (x) - 2 x - a ， x \leq 0 ， \\ | l o g_{2} x | - a - 1 ， x > 0 \end{array}$ 有3个零点，则 $a$ 的取值范围为（）

A、 $(2 ， 3]$ B、 $(- 1 ， 3]$ C、 $(3 ， 4]$ D、 $(- 1 ， 4]$

查看试题解析
4. 已知函数 $f (x) = a x^{3} + b x + 1$ ，若 $f (x)$ 存在零点 $x_{0} < - 1$ ，且满足 $f^{'} (x_{0}) = f (x_{0})$ ，则（）

A、 $\frac{1}{a} + \frac{3}{b} < 0$ B、 $a b > 0$ C、 $3 a + b < 0$ D、 $a + b > 1$

查看试题解析
5. 已知函数 $f (x) = s i n (ω x + \frac{π}{6}) (ω > 0)$ 在 $[0 ， 2 π]$ 上有且仅有4个零点，则 $ω$ 的取值范围是（）

A、 $[\frac{23}{12} ， \frac{29}{12}]$ B、 $[\frac{23}{12} ， \frac{29}{12})$ C、 $(\frac{11}{30} ， \frac{11}{24}]$ D、 $[\frac{11}{30} ， \frac{11}{24})$

查看试题解析
6. 已知函数 $f (x) = s i n (\frac{\sqrt{a x^{3} + b x + b}}{x} \cdot π) - 1 ， a \geq 0$ 在 $(1 ， + \infty)$ 上有且仅有1个零点，则下列选项中b的可能取值为（）

A、0 B、 $\frac{1}{8}$ C、 $\frac{1}{2}$ D、4

查看试题解析
7. 已知 $f (x)$ 是定义在 $[- 10 ， 10]$ 上的奇函数，且 $f (x) = f (4 - x)$ ，则函数 $f (x)$ 的零点个数至少为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 设函数 $f (x)$ 的定义域为 $R$ ，则“ $f (x)$ 是 $R$ 上的增函数”是“任意 $a > 0$ ， $y = f (x + a) - f (x)$ 无零点”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
9. 已知函数 $f (x) = x^{3} + b x^{2} + c x$ 的图象如图所示，则 $x_{1} \cdot x_{2}$ 等于（）

A、2 B、 $\frac{4}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
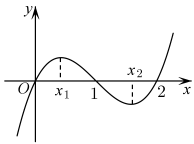10. 设函数 $f (x) = | 2 x - 1 |$ ，函数 $g (x) = f (f (x)) - l o g_{a} (x + 1)$ ， $(a > 0 ， a \neq 1)$ 在[0，1]上有3个不同的零点，则实数 $a$ 的取值范围为（）

A、 $(1 ， \frac{3}{2})$ B、（1，2） C、 $(\frac{3}{2} ， 2)$ D、 $(2 ， + \infty)$

查看试题解析
11. 已知函数 $f (x) = {\begin{array}{l} 1 - | 1 - x | ， 0 \leq x \leq 2 \\ 2 f (x - 2) ， x > 2 \end{array}$ ，当 $x \in [0 ， 8]$ 时，函数 $F (x) = f (x) - k x$ 恰有六个零点，则实数 $k$ 的取值范围是（）

A、 $(\frac{4}{5} ， 1)$ B、 $(\frac{2}{3} ， \frac{4}{5})$ C、 $[\frac{2}{3} ， \frac{4}{5})$ D、 $[\frac{4}{5} ， 1)$

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} 10 x - m ， x \leq \frac{1}{2} \\ x e^{x} - 2 m x + m ， x > \frac{1}{2} \end{array}$ （e是自然对数的底数）在定义域R上有三个零点，则实数m的取值范围是（）

A、 $(e ， + \infty)$ B、 $(e ， 5]$ C、 $(e ， 5)$ D、 $[e ， 5]$

查看试题解析
13. 已知函数 $f (x) = 2 a e^{x} - e^{a} x^{2}$ 至多有2个不同的零点，则实数a的最大值为（）．

A、0 B、1 C、2 D、e

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} e x l n x ， x > 0 \\ x^{3} - 3 x ， x \leq 0 \end{array}$ ，若函数 $y = {[f (x)]}^{2} - 1$ 与 $y = a f (x)$ 的图象恰有6个不同的公共点，则实数a的取值范围是（）

A、 $(0 ， \frac{3}{2})$ B、 $(0 ， \frac{7}{2})$ C、 $(1 ， \frac{7}{2})$ D、 $(1 ， + \infty)$

查看试题解析
15. 已知函数 $f (x) = | l o g_{2} x | ， g (x) = {\begin{array}{l} 0 ， 0 < x \leq 1 \\ | x - 2 | - 0.5 ， x > 1 \end{array}$ ，则方程 $| f (x) - g (x) | = 1$ 的实根个数为（）个．

A、1 B、2 C、3 D、4

查看试题解析
16. 定义在R上的偶函数 $f (x)$ 满足 $f (2 - x) = f (x + 2)$ ，当 $x \in [0 ， 2]$ 时 $f (x) = {(\sqrt{e})}^{x}$ ，若在区间 $x \in [0 ， 10]$ 内，函数 $g (x) = f (x) - (x + 1)^{m}$ 有个5零点，则实数m的取值范围是（）

A、 $(0 ， l o g_{11} e)$ B、 $(0 ， l o g_{11} e) ∪ (\frac{1}{2} ， l o g_{7} e)$ C、 $(l o g_{11} e ， \frac{1}{2})$ D、 $(l o g_{11} e ， \frac{1}{2}) ∪ (\frac{1}{2} ， l o g_{7} e)$

查看试题解析

二、多选题

17. 已知函数 $f (x) = a^{x} - x^{a} (a > 1)$ 的定义域为 $(0 ， + \infty)$ ，且 $f (x)$ 仅有一个零点，则（）

A、e是 $f (x)$ 的零点 B、 $f (x)$ 在 $(1 ， e)$ 上单调递增 C、 $x = 1$ 是 $f (x)$ 的极大值点 D、 $f (e)$ 是 $f (x)$ 的最小值

查看试题解析
18. 已知函数 $f (x) = 2 x - c o s x$ 的零点为 $x_{0}$ ，则（）

A、 $x_{0} < \frac{1}{2}$ B、 $x_{0} > \frac{1}{3}$ C、 $t a n x_{0} > \frac{\sqrt{5}}{2}$ D、 $x_{0} - \frac{1}{4} < s i n x_{0}$

查看试题解析

三、填空题

19. 设 $a ， b ， c \in R ， a \neq 0$ ，若函数 $y = a x^{2} + b x + c$ 有且仅有一个零点，且 $2 a^{2} + 3 a b + 8 a c = 1$ ，则 $a + b$ 的最小值为， $a + b + a b$ 的最小值为．

查看试题解析
20. 已知函数 $y = f (x)$ 是定义域为R的偶函数，当 $x \geq 0$ 时， $f (x) = {\begin{array}{l} (\frac{1}{2})^{x} ， \\ l o g_{16} x ， \end{array}$ $\begin{array}{l} 0 \leq x < 2 \\ x \geq 2 \end{array}$ ，若关于x的方程 $[f (x)]^{2} + a f (x) + b = 0 (a ， b \in R)$ 有且仅有7个不同实数根，则 $a + b =$

查看试题解析
21. 已知函数 $f (x) = {\begin{array}{l} e^{x} - a x ， x \geq 0 ， \\ a x^{3} - 2 x + 1 ， x < 0 . \end{array}$ 当 $a = 0$ 时， $f [f (- \frac{1}{2})] =$ ，若函数 $f (x)$ 有3个不同的零点，则 $a$ 的取值范围是．

查看试题解析
22. 设 $a \in R$ ．函数 $f (x) = {\begin{array}{l} 2 e^{x} - 1 ， & x \leq 0 \\ a x^{2} + (a^{2} - 2) x - l n x ， & x > 0 \end{array}$ ，若 $f (f (0)) = 0$ ，则 $a =$ ，若 $f (x)$ 只有一个零点，则a $的$ 取值范围是．

查看试题解析
23. 函数 $f (x) = {\begin{array}{l} x^{3} + 2 ， x \leq 0 \\ x - 3 + e^{x} ， x > 0 \end{array}$ 的零点个数为.

查看试题解析
24. 若函数 $f (x) = {\begin{array}{l} 2^{x} - b ， x < 0 ， \\ \sqrt{x} ， x \geq 0 \end{array}$ 有且仅有两个零点，则实数 $b$ 的一个取值为.

查看试题解析
25. 已知函数 $f (x) = 2^{| x |} + x^{2} + a$ .
①对于任意实数 $a$ ， $f (x)$ 为偶函数；
②对于任意实数 $a$ ， $f (x)$ 在 $(- \infty ， 0)$ 上单调递减，在 $(0 ， + \infty)$ 上单调递增；
③存在实数 $a$ ，使得 $f (x)$ 有3个零点；
④存在实数 $a$ ，使得关于 $x$ 的不等式 $f (x) \geq 2022$ 的解集为 $(- \infty ， - 1] ∪$ $[1 ， + \infty)$ .
所有正确命题的序号为.

查看试题解析
26. 已知函数 $f (x)$ 满足 $f (x - 2) = f (x + 2) ， 0 \leq x < 4$ 时， $f (x) = \sqrt{4 - (x - 2)^{2}}$ ， $g (x) = f (x) - k_{n} x (n \in N^{*} ， k_{n} > 0)$ ．若函数 $g (x)$ 的图像与x轴恰好有 $2 n + 1$ 个不同的交点，则 $k_{1}^{2} + k_{2}^{2} + \cdot \cdot \cdot + k_{n}^{2} =$ ．

查看试题解析
27. 已知 $f (x)$ 是定义在 $R$ 上的奇函数，其图象关于点 $(2 ， 0)$ 对称，当 $x \in [0 ， 2]$ 时， $f (x) = - \sqrt{1 - (x - 1)^{2}}$ ，若方程 $f (x) - k (x - 2) = 0$ 的所有根的和为6，则实数 $k$ 的取值范围是．

查看试题解析
28. 声音是由于物体的振动产生的能引起听觉的波，其中包含着正弦函数.纯音的数学模型是函数 $y = A s i n ϖ t$ .我们听到的声音是由纯音合成的，称为复合音.已知一个复合音的数学模型是函数 $f (x) = s i n x + \frac{1}{2} s i n 2 x$ .给出下列四个结论：
① $f (x)$ 的最小正周期是 $π$ ；
② $f (x)$ 在 $[0 ， 2 π]$ 上有3个零点；
③ $f (x)$ 在 $[0 ， \frac{π}{2}]$ 上是增函数；
④ $f (x)$ 的最大值为 $\frac{3 \sqrt{3}}{4}$ .
其中所有正确结论的序号是.

查看试题解析

四、解答题

29. 设函数 $f (x) = - \frac{1}{2} x^{2} + (a - 1) x + a l n x + \frac{a}{2}$ ， $a > 0$ ．

(1)、若 $a = 1$ ，求函数 $f (x)$ 的单调区间和最值；

(2)、求函数 $f (x)$ 的零点个数，并说明理由．

查看试题解析
30. 已知 $a > 0$ ，设函数 $f (x) = (2 x - a) l n x + x ， f^{'} (x)$ 是 $f (x)$ 的导函数．

(1)、若 $a = 2$ ，求曲线 $f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、若 $f (x)$ 在区间 $(1 ， + \infty)$ 上存在两个不同的零点 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，
①求实数a范围；
②证明： $\frac{x_{2} f^{'} (x_{2})}{x_{1} - 1} < \frac{(a - e) (a - 2 e) (a - 3)}{2 e}$ ．
注，其中 $e = 2.71828 \cdot \cdot \cdot \cdot \cdot \cdot$ 是自然对数的底数．

查看试题解析
31. 已知函数 $f (x) = x l n x + a ， (a \in R)$ ．

(1)、求函数 $f (x)$ 的单调区间；

(2)、当 $0 < a < \frac{1}{e}$ 时，证明：函数 $f (x)$ 有两个零点；

(3)、若函数 $g (x) = f (x) - a x^{2} - x$ 有两个不同的极值点 $x_{1} ， x_{2}$ （其中 $x_{1} < x_{2}$ ），证明： $x_{1} \cdot {x_{2}}^{2} > e^{3}$ ．

查看试题解析
32. 已知函数 $f (x) = e^{x} - x l n x - a x - 1 (a \in R)$ 有两个零点．

(1)、求a的取值范围；

(2)、设 $x_{1} ， x_{2}$ 是 $f (x)$ 的两个零点，证明： $x_{1} + x_{2} > 2$ ．

查看试题解析
33. 已知函数 $f (x) = m l n x - x e^{x} + x$ ．

(1)、若 $m = 1$ ，求 $f (x)$ 的最大值；

(2)、若 $f (x_{1}) + x_{1} e^{x_{1}} + m = 0 ， f (x_{2}) + x_{2} e^{x_{2}} + m = 0$ ，其中 $x_{1} \neq x_{2}$ ，求实数 $m$ 的取值范围．

查看试题解析
34. 已知函数 $f (x) = l n x + \frac{a}{x}$ 的极小值为1．

(1)、求实数a的值；

(2)、设函数 $g (x) = f (x) - \frac{1}{x} + m (\frac{1}{x^{2}} - 1)$ ．
①证明：当 $0 < m < \frac{1}{2}$ 时， $\forall x \in (0 ， \frac{m}{1 - m})$ ， $g (x) > 0$ 恒成立；
②若函数 $g (x)$ 有两个零点，求实数m的取值范围．

查看试题解析
35. 已知函数 $f (x) = x^{2} \cdot \ln x$ .
（Ⅰ）求函数 $y = f (x) - x$ 的最小值；

（Ⅱ）若方程 $f (x) = m (m \in R)$ 有两实数解 $x_{1} ， x_{2}$ ，求证： $\frac{1}{x_{1}^{2}} + \frac{1}{x_{2}^{2}} > \frac{e + 1}{1 - | x_{1} - x_{2} |}$ .（其中 $e = 2.71828 \dots$ 为自然对数的底数）.

查看试题解析
36. 已知函数 $f (x) = \frac{1}{2} (a - 1) x^{2} + a x - 2 l n x$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、当 $a = 1$ 时， $g (x) = f (\sqrt{x})$ ，若 $m \leq 3 - 4 l n 2$ ，求证：对于任意 $k > 0$ ，函数 $h (x) = \frac{g (x) - m}{x} - k$ 有唯一零点．

查看试题解析