3.3函数的奇偶性、周期性与对称性——2023年高考数学一轮复习(新高考地区专用)
试卷更新日期:2022-07-14 类型:一轮复习
一、单选题
-
1. 已知函数是偶函数,的图象关于直线l对称,则直线l的方程为( )A、 B、 C、 D、2. 已知函数的部分图象如图所示,则的解析式可能是( )
 A、 B、 C、 D、3. 函数的图象大致为( )A、
A、 B、 C、 D、3. 函数的图象大致为( )A、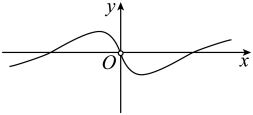
B、
B、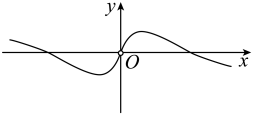
C、
C、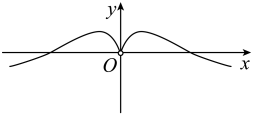
D、
D、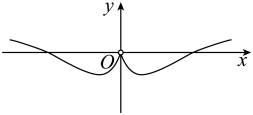
4. 函数在上的大致图象为( )A、
4. 函数在上的大致图象为( )A、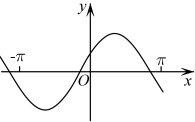 B、
B、 C、
C、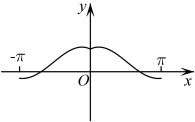 D、
D、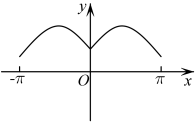 5. 函数 , 将函数的图象向左平移个单位长度,得到函数的图象,若为偶函数,则的最小值是( )A、 B、 C、 D、6. 若是奇函数,则( )A、 B、 C、 D、7. 已知偶函数在上单调递增,且 , 则不等式的解集为( )A、 B、 C、 D、8. 若函数 , 设 , , , 则下列选项正确的是( )A、 B、 C、 D、9. 如图为函数的部分图象,则的值可能是( )
5. 函数 , 将函数的图象向左平移个单位长度,得到函数的图象,若为偶函数,则的最小值是( )A、 B、 C、 D、6. 若是奇函数,则( )A、 B、 C、 D、7. 已知偶函数在上单调递增,且 , 则不等式的解集为( )A、 B、 C、 D、8. 若函数 , 设 , , , 则下列选项正确的是( )A、 B、 C、 D、9. 如图为函数的部分图象,则的值可能是( )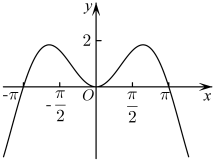 A、4 B、3 C、2 D、110. 已知是定义在上的奇函数,且 , 则函数的零点个数至少为( )A、3 B、4 C、5 D、611. 已知函数满足:对任意 , . 当时, , 则( )A、 B、 C、 D、12. 已知函数是定义在上的偶函数,且在单调递增,记 , , , 则a,b,c的大小关系为( ).A、 B、 C、 D、13. 已知偶函数在区间上单调递减.若 , 则x的取值范围是( )A、 B、 C、 D、14. 已知函数 , 其图象大致为( )A、
A、4 B、3 C、2 D、110. 已知是定义在上的奇函数,且 , 则函数的零点个数至少为( )A、3 B、4 C、5 D、611. 已知函数满足:对任意 , . 当时, , 则( )A、 B、 C、 D、12. 已知函数是定义在上的偶函数,且在单调递增,记 , , , 则a,b,c的大小关系为( ).A、 B、 C、 D、13. 已知偶函数在区间上单调递减.若 , 则x的取值范围是( )A、 B、 C、 D、14. 已知函数 , 其图象大致为( )A、 B、
B、 C、
C、 D、
D、 15. 下列函数中,既是偶函数又在 , 上单调递增的函数是( )A、 B、 C、 D、16. 定义在上的奇函数满足为偶函数,且当时, , 则下列结论正确的是( )A、 B、 C、 D、17. 设 是定义在R上的奇函数,且当 时, ,则 的解集为( )A、 B、 C、 D、18. 已知函数 ,则对任意实数 , ,“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件19. 已知函数 是偶函数,其导函数 的图象见下图,且 对 恒成立,则下列说法正确的是( )
15. 下列函数中,既是偶函数又在 , 上单调递增的函数是( )A、 B、 C、 D、16. 定义在上的奇函数满足为偶函数,且当时, , 则下列结论正确的是( )A、 B、 C、 D、17. 设 是定义在R上的奇函数,且当 时, ,则 的解集为( )A、 B、 C、 D、18. 已知函数 ,则对任意实数 , ,“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件19. 已知函数 是偶函数,其导函数 的图象见下图,且 对 恒成立,则下列说法正确的是( )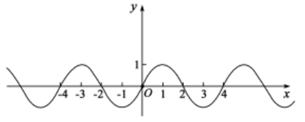 A、 B、 C、 D、20. 函数 在 单调递减,且为偶函数.若 ,则满足 的 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、20. 函数 在 单调递减,且为偶函数.若 ,则满足 的 的取值范围是( )A、 B、 C、 D、二、多选题
-
21. 若函数同时具有性质:①对于任意的 , , ②为偶函数,则函数可能为( )A、 B、 C、 D、22. 已知三次函数 , 若函数的图象关于点(1,0)对称,且 , 则( )A、 B、有3个零点 C、的对称中心是 D、23. 若函数()是周期为2的奇函数.则下列选项一定正确的是( )A、函数的图象关于点对称 B、2是函数的一个周期 C、 D、24. 已知函数 , , , 则( )A、的图象关于对称 B、的图象没有对称中心 C、对任意的 , 的最大值与最小值之和为 D、若 , 则实数的取值范围是25. 已知函数 , . 若实数a,b(a,b均大于1)满足 , 则下列说法正确的是( )A、函数在R上单调递增 B、函数的图象关于中心对称 C、 D、26. 已知定义域为的偶函数在上单调递增,且 , 使 . 则下列函数中符合上述条件的是( )A、 B、 C、 D、
三、填空题
-
27. 已知 是定义为R的奇函数,当 , ,则 .28. 设函数 , 则 , 若 , 则实数a的最大值为 .29. 已知定义在R上的函数和函数满足 , 且对于任意x都满足 , 则 .30. 已知函数.
①对于任意实数 , 为偶函数;
②对于任意实数 , 在上单调递减,在上单调递增;
③存在实数 , 使得有3个零点;
④存在实数 , 使得关于的不等式的解集为.
所有正确命题的序号为.