3.1函数的概念与表示——2023年高考数学一轮复习(新高考地区专用)
试卷更新日期:2022-07-14 类型:一轮复习
一、单选题
-
1. 函数的定义域为( )A、 B、 C、 D、2. 已知函数与的图象上存在关于轴对称的点,则的取值范围是( )A、 B、 C、 D、3. 已知对数函数的图像经过点与点 , , , , 则( )A、 B、 C、 D、4. 函数 的定义域为( )A、 B、 C、 D、5. 函数的图象如图所示,则f(x)的解析式可能是( )
 A、 B、 C、 D、6. 已知函数的图象如图所示,则的解析式可能是( )(是自然对数的底数)
A、 B、 C、 D、6. 已知函数的图象如图所示,则的解析式可能是( )(是自然对数的底数) A、 B、 C、 D、7. 已知集合 , , 则( )A、 B、 C、 D、8. 已知函数满足 , 当时, , 那么( )A、 B、 C、 D、9. 下列函数中,定义域与值域均为R的是( )A、 B、 C、 D、10. 若函数 , 则函数的最小值为( )A、-1 B、-2 C、-3 D、-411. 已知函数 , 则( )A、1 B、2 C、3 D、412. 已知函数图象相邻两条对称轴之间的距离为 , 将函数的图象向左平移个单位后,得到的图象关于轴对称,那么函数的图象( )A、关于点对称 B、关于点对称 C、关于直线对称 D、关于直线对称13. 函数的图象大致为( )A、
A、 B、 C、 D、7. 已知集合 , , 则( )A、 B、 C、 D、8. 已知函数满足 , 当时, , 那么( )A、 B、 C、 D、9. 下列函数中,定义域与值域均为R的是( )A、 B、 C、 D、10. 若函数 , 则函数的最小值为( )A、-1 B、-2 C、-3 D、-411. 已知函数 , 则( )A、1 B、2 C、3 D、412. 已知函数图象相邻两条对称轴之间的距离为 , 将函数的图象向左平移个单位后,得到的图象关于轴对称,那么函数的图象( )A、关于点对称 B、关于点对称 C、关于直线对称 D、关于直线对称13. 函数的图象大致为( )A、 B、
B、 C、
C、 D、
D、 14. 函数 在 上的图象大致为( )A、
14. 函数 在 上的图象大致为( )A、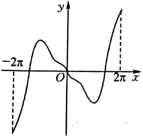 B、
B、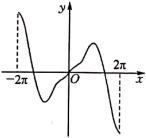 C、
C、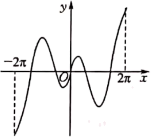 D、
D、 15. 下图中的函数图象所对应的解析式可能是( )
15. 下图中的函数图象所对应的解析式可能是( ) A、 B、 C、 D、16. 对于函数 ,下列结论正确的是( )A、图象关于点 对称 B、在区间 上单调递增 C、与函数 相等 D、在区间 的最大值为217. 设函数则不等式的解集为( )A、 B、 C、 D、18. 已知 ,则函数 的图象不可能是( )A、
A、 B、 C、 D、16. 对于函数 ,下列结论正确的是( )A、图象关于点 对称 B、在区间 上单调递增 C、与函数 相等 D、在区间 的最大值为217. 设函数则不等式的解集为( )A、 B、 C、 D、18. 已知 ,则函数 的图象不可能是( )A、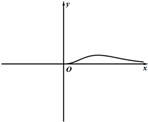 B、
B、 C、
C、 D、
D、 19. 已知函数 , 则方程的实根个数为( )个.A、1 B、2 C、3 D、420. 定义在R上的函数f(x)满足 , 且当时, . 若对任意 , 都有 , 则m的取值范围是( )A、[ , +∞) B、[ , +∞) C、[ , +∞) D、[ , +∞)
19. 已知函数 , 则方程的实根个数为( )个.A、1 B、2 C、3 D、420. 定义在R上的函数f(x)满足 , 且当时, . 若对任意 , 都有 , 则m的取值范围是( )A、[ , +∞) B、[ , +∞) C、[ , +∞) D、[ , +∞)二、填空题
-
21. 已知函数的定义域为R,且满足 , 当时,若 , 则实数 , .22. 函数的值域为.23. 已知函数 , 若 , 则实数 .24. 已知函数 , 若均不相等,且 , 则的取值范围是25. 已知偶函数是实数集上的周期为2的周期函数,当时, , 则当时, .26. 若分段函数 , 将函数 , 的最大值记作 , 那么当时,的取值范围是;