（沪教版）2022年暑假八年级数学复习巩固专题11 事件的概率
试卷更新日期：2022-07-13 类型：复习试卷
一、单选题
-
1. “黄梅时节家家雨，青草池塘处处蛙.”如图，梅雨时节的苏州，粉墙黛瓦、小桥流水，宛如一幅水墨诗画.某天，气象台预报明天降雨的概率是90%，则以下判断正确的是（ ）
A、明天一定会下雨 B、明天有90%的地区会降雨 C、明天有90%的时间会下雨 D、明天下雨的可能性很大2. 下图中的转盘被划分成六个相同的扇形，并分别标上1，2，3，4，5， 6这六个数字，指针停在每个扇形.上的可能性相等，四位同学各自发表了下述见解：甲：如果指针前三次都停在3号扇形，下一次就一定不会停在3号扇形；
乙：只要指针连续转六次，一定会有一次停在6号扇形；
丙：指针停在奇数号扇形的可能性与停在偶数号扇形的可能性相同；
丁：运气好的时候，只要在转动前默默想好让指针停在6号扇形，指针停在6号扇形的可能性就会加大.其中你认为正确的见解有（ ）.
A、1个 B、2个 C、3个 D、4个3. 下列说法正确的是（ ）.A、“明天降 雨的概率是80%”表示明天有80%的时间都在降雨 B、“抛一枚硬币正面朝上的概率为 "表示每抛两次就有一次正面朝上 C、“彩票中奖的概率为1%”表示买100张彩票肯定会中奖 D、“抛一枚均匀的正方体骰子，朝上的点数是2的概率为 ”表示随着抛掷次数的增加，“抛出朝上的点数是2"这一事件发生的频率稳定在附近4. 下列说法正确的是（ ）A、扔100次硬币，都是国徽面向上，是不可能事件 B、小芳在扔图钉游戏中，扔10次，有6次都是钉尖朝下，所以钉尖朝下的可能性大 C、王明同学一直是级部第一名，他能考上重点高中是必然事件 D、投掷一枚均匀的骰子，投出的点数是10，是一个确定事件5. 下列有四种说法：①了解某一天出入扬州市的人口流量用普查方式最容易；
②“在同一年出生的367名学生中，至少有两人的生日是同一天”是必然事件；
③“打开电视机，正在播放少儿节目”是随机事件；
④如果一件事发生的概率只有十万分之一，那么它仍是可能发生的事件．
其中，正确的说法是（ ）
A、①②③ B、①②④ C、①③④ D、②③④6. 嘉琪在做“抛一枚正六面体骰子”的实验时，他连续抛了10次，其中“6”点向上共出现3次，则出现“6”点向上的频率是（ ）A、 B、 C、 D、7. 如图，有两个可以自由转动的转盘（每个转盘均被等分），同时转动这两个转盘，待转盘停止后，两个指针同时指在偶数上的概率是（ ）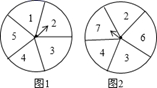
A、 B、 C、 D、8. 在四边形 中，从以下四个条件中：① ② ③ ④ ，其中任选两个能判定四边形ABCD为平行四边形的概率为（ ）A、 B、 C、 D、9. 甲、乙两位同学在一次实验中统计了某一结果出现的频率，给出的统计图如图所示，则符合这一结果的实验可能是（ ）
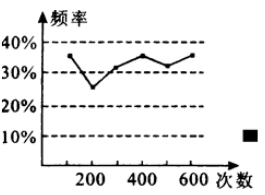A、掷一枚正六面体的骰子，出现5点的概率 B、掷一枚硬币，出现正面朝上的概率 C、任意写出一个整数，能被2整除的概率 D、一个袋子中装着只有颜色不同，其他都相同的 两个红球和一个黄球，从中任意取出一个是黄球的概率10. “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形．如图，是一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4．小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是（ ）
A、 B、 C、 D、二、填空题
-
11. 在做“抛掷一枚质地均匀的硬币”试验时，下列说法正确的是.
①不同次数的试验，正面向上的频率可能会不相同
②当抛掷的次数 很大时，正面向上的次数一定为
③多次重复试验中，正面向上发生的频率会在某个常数附近摆动，并趋于稳定
④连续抛掷 次硬币都是正面向上，第 次抛掷出现正面向上的概率小于
12. 小丽掷一枚质地均匀的硬币 次，有 次正面朝上，当她掷第 次时，正面朝上的概率为.13. 小芳抛一枚硬币10次，有6次正面朝上，当她抛第11次时，正面朝上的概率为 ．14. 在一个不透明的袋中装有除颜色外其余均相同的 个小球，其中有6个黑球，从袋中随机摸出一球，记下其颜色，称为一次摸球试验，之后把它放回袋中，搅匀后，再继续摸出一球，利用计算机模拟的结果，摸出黑球的频率在0.5附近波动，由此可以估计出 的值是.15. 如图是一张矩形纸板，顺次连接各边中点得到菱形，再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上，则飞镖落在阴影区域的概率是.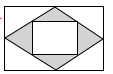
三、解答题
-
16. 一个不透明的口袋中装有2个红球、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．17. 小强和小明两个同学设计一种同时向上抛出1元硬币的游戏，游戏规则如下：如果抛出的硬币落下后朝上的两个面都为1元，则小强得1分，其余情况小明得1分，谁先得到10分谁就赢得比赛.你认为这个游戏规则公平吗?若不公平，怎样改正?18. 抢30游戏:抢30游戏的规则是:第一个先说“1”或“1,2”,第二个人要接着往下说一个或两个数,然后又轮到第一个人，再接着往下说一个或两个数,这样两人反复轮流,每人每次说一个或两个数,但不可以不说或说三个数,谁先抢说到30,谁就获胜!该游戏公平吗?说说你的理由.19. 2020年冬奥会将在延庆召开，延庆区某中学响应区团委的号召，组织学生参加“我是奥运小志愿者”活动，志愿者可以到“八达岭长城”、“世葡园”、“龙庆峡”、“百里画廊”四个景区之一参加活动．晓明对“八达岭长城”和“百里画廊”最感兴趣，他将四个景区编号为A、B、C、D，并写在四张卡片上（除编号和内容不同之外，其余完全相同），他将卡片背面朝上，洗匀放好，从中随机抽取两张，请用列表或是画树状图的方法，求抽到的两张卡片恰好是“八达岭长城”，“百里画廊”的概率．（说明：这四张卡片分别用它的编号A、B、C、D表示）
四、综合题
-
20. 如图，分别转动甲、乙、丙、丁四个转盘，当转盘停止后，
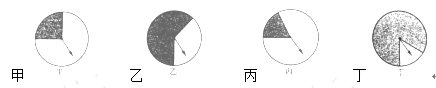(1)、哪个转盘的指针指向阴影区域的可能性最大？(2)、哪个转盘的指针指向阴影区域的可能性最小？(3)、若设 、 、 、 分别表示甲、乙、丙、丁四个转盘的指针指向阴影区域，用“<”把指向阴影区域的概率 、 、 、 连接起来.21. 一只不透明的袋子中装有1个红球、2个绿球和3个白球，每个球除颜色外都相同．将球搅匀后，从中任意摸出一球．
(1)、会有哪些等可能的结果；(2)、你认为摸到哪种颜色的球可能性最大？摸到哪种颜色的球可能性最小？22. 热情的刘老师邀请两位朋友小高和小新来苏州游玩，他向两人推荐了四个游览地：苏州乐园、太湖湿地公园、白马涧龙池景区和淮海街，并做成四个外形完全一致的纸签让两位朋友随机抽取.(1)、若小高先抽中了“苏州乐园”（不放回），则小新再抽签时选择“太湖湿地公园”的概率是 ：(2)、若小高先抽签后立即放回，再由小新抽签，求两人抽取到同一个景点的概率.23. 经过某十字路口的汽车，可能直行，也可能向左转或向右转．如果这三种可能性大小相同，求两辆车经过这个十字路口时，下列事件的概率：(1)、两辆车中恰有一辆车向左转；(2)、两辆车行驶方向相同．24. 甲、乙两同学玩转盘游戏时，把质地相同的两个盘A、B分别平均分成2份和3份，并在每一份内标有数字如图.游戏规则：甲、乙两同学分别同时转动两个转盘各1次，当转盘停止后，指针所在区域的数字之积为偶数时甲胜；数字之积为奇数时乙胜.若指针恰好在分割线上，则需要重新转动转盘.
(1)、用树状图或列表的方法，求甲获胜的概率；(2)、这个游戏规则对甲、乙双方公平吗？请判断并说明理由