（沪教版）2022年暑假八年级数学复习巩固专题8 梯形
试卷更新日期：2022-07-13 类型：复习试卷
一、单选题
-
1. 梯形ABCD中，AD// BC ，AB=3，BC=4，CD=2， AD=1，则梯形的面积为 （ ）
A、 B、 C、 D、2. 如图，在梯形ABCD中，AB∥CD，AD=DC=CB，AC⊥BC，那么下列结论不正确的是（ ）
A、AC=2CD B、DB⊥AD C、∠ABC=60° D、∠DAC=∠CAB3. 如图，在▱ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE于G，BG= ，则梯形AECD的周长为（ ）
A、22 B、23 C、24 D、254. 如图所示，有一个含60°角的直角三角形纸片，沿其斜边和长直角边中点剪开后，不能拼成的四边形是（ ）
A、邻边不相等的矩形 B、等腰梯形 C、有一角是锐角的菱形 D、正方形5. 已知四边形 中， ，下列判断中的正确的是（ ）A、如果 ，那么四边形 是等腰梯形 B、如果 ，那么四边形 是菱形 C、如果AC平分BD，那么四边形 是矩形 D、如果 ，那么四边形 是正方形6. 我们把梯形下底与上底的差叫做梯形的底差，梯形的高与中位线的比值叫做梯形的纵横比．如果一个腰长为 的等腰梯形，底差等于 ，面积为 ，那么这个等腰梯形的纵横比等于（ ）A、 B、 C、 D、7. 如图，在▱ABCD中，AB＝6，AD＝8，将△ACD沿对角线AC折叠得到△ACE，AE与BC交于点F，则下列说法正确的是（ ）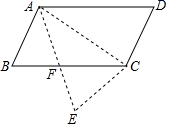
A、当∠B＝90°时，则EF＝2 B、当F恰好为BC的中点时，则▱ABCD的面积为12 C、在折叠的过程中，△ABF的周长有可能是△CEF的2倍 D、当AE⊥BC时，连结BE，四边形ABEC是菱形8. 如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点.若OE=3，则AB的长为（ ）
A、3 B、6 C、9 D、129. 若顺次连接四边形各边中点所得的四边形是菱形，则原四边形（ ）A、一定是矩形 B、一定是菱形 C、对角线一定互相垂直 D、对角线一定相等10. 如图，在▱ABCD中，对角线AC，BD交于点O，点E是BC的中点。若OE=3cm，则AB的长为（ ）
A、3cm B、6cm C、9cm D、12cm二、填空题
-
11. 梯形的面积为 平方厘米，中位线长为 厘米，则这个梯形的高为厘米．12. 在直角梯形 中， ， ， ， ，则 的度数是 ．13. 如果等腰梯形的一个底角为120°，这个等腰梯形的上、下底长分别为6和10，那么这个等腰梯形的腰长为 ．14. 已知长分别为14，13，9，7的四条线段可以构成梯形，则在所有可能构成的梯形中，连接梯形两腰中点的线段长度的最大值是.15. 如图，菱形ABCD中，对角线AC，BD相交于点O.H为AD边的中点，菱形ABCD的周长为40，则OH的长等于.
三、解答题
-
16. 如图，在梯形ABCD中，AD∥BC，∠B=45°，AD=8，AB= ， CD=26，求BC的长．
17. 如图，在梯形 中， ， ， ， ．点 为边 的中点，过点 作 交 于点 ，求线段 的长．
18. 已知：如图，梯形ABCD中，AD∥BC，∠B=60°，∠C=30°，AD=4，BC=10.求：梯形两腰AB、CD的长.
19. 已知：如图， 是 的中线， 是线段 的中点， .求证：四边形 是等腰梯形.
20. 如图，梯形ABCD中，AB//CD，AD=BC，延长AB到E，使BE=DC，连结AC、CE.求证AC=CE.
21. 如图，在等腰梯形ABCD中，DC∥AB，AD=BC=2，BD平分∠ABC．∠A=60°，求对角线BD的长和梯形ABCD的面积．
