（沪教版）2022年暑假八年级数学复习巩固专题7 平行四边形
试卷更新日期：2022-07-13 类型：复习试卷
一、单选题
-
1. 在 ▱ABCD 中，∠A+∠B+∠C=210°，则∠B的度数是（ ）A、150° B、110° C、70° D、30°2. 如图，在平行四边形ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F，若∠B＝52°，∠DAE＝20°，则∠FED′的大小为（ ）
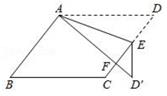A、26° B、36° C、46° D、56°3. 下列条件中，能判定四边形是平行四边形的条件是（ ）A、一组对边平行，另一组对边相等 B、一组对边平行，一组对角相等 C、一组对边平行，一组邻角互补 D、一组对边相等，一组邻角相等4. 下列条件中不能判定四边形是平行四边形的是（ ）A、 ， B、 ， C、 ， D、 ，5. 如图，四边形 是平行四边形，对角线 与BD相交于点 ，若 ， ， ，则 的周长是（ ）
A、15 B、17 C、20 D、256. 已知▱ABCD的周长为34cm，两邻边之差3cm，则两邻边长分别为 （ ）A、10cm，7cm B、11cm，6cm C、12cm，5cm D、18.5cm，15.5cm7. 如图，在正方形ABCD中，点M、N分别为边CD、BC上的点，且DM=CN，AM与DN交于点P，连接AN，点Q为AN的中点，连接PQ、BQ，若AB=8，DM=2，给出以下结论：①AM⊥DN；②∠MAN=∠BAN；③△PQN≌△BQN；④PQ=5。其中正确的结论有（ ）（填上所有正确结论的序号）
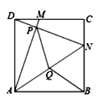A、②③ B、①④ C、①②③ D、①②③④8. 如图.已知正方形ABCD的边长为12，BE＝EC，将正方形的边CD沿DE折叠到DF，延长EF交AB于G，连接DG.现有如下3个结论；①AG+EC＝GE；②∠GDE＝45°；③△BGE的周长是24.其中正确的个数为（ ）
A、0 B、1 C、2 D、39. 把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为（ ）.
A、6 B、8 C、12 D、2410. 顺次连接矩形的各边中点，所得的四边形一定是（ ）A、正方形 B、菱形 C、矩形 D、梯形二、填空题
-
11. 如图，在平行四边形OABC中，对角线相交于点E，OA边在x轴上，点O为坐标原点，已知点 ， ，则点C的坐标为
12. 如图，在▱ABCD中，对角线AC，BD相交于点O，∠BAC＝90°，AD＝15，OC＝6，则△BOC的面积为 ．
13. 如图，在 ABCD中，AE⊥BC于E，AC=AD，∠CAE=56°，则∠D= ．
14. 如图，在菱形ABCD中，AC=6，BD=4，则AB=
15. 如图，O是正方形ABCD对角线交点，E是线段AO上一点，若AB=1，∠BED=135°，则AE的长为
三、解答题
-
16. 用反证法证明下列问题。
如图，在△ABC中，点D，E分别在AC，AB上，BD，CE相交于点O。
求证：BD和CE不可能互相平分。
17. 如图所示，在四边形ABCD中，M是边BC的中点，AM，BD互相平分并交于点O。求证：四边形AMCD是平行四边形。
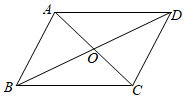
18. 如图，平行四边形 的对角线 与 相交于点 ，点 为 的中点，过点 作 交 的延长线于点 ，连接 .求证：四边形 是平行四边形.
19. 如图，在 中，点 ， 分别是 ， 上的点，且 ，分别过点 ， 作 ， ，垂足分别为 ， ，连接 ， .求证：四边形 是平行四边形.
20. 如图，四边形ABCD中，AD∥BC ，AC、BD相交于点O，O是AC的中点.求证：四边形ABCD是平行四边形.
21. 操作：第一步：如图1，对折长方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开.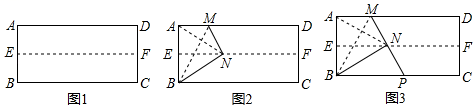
第二步：如图2，再一次折叠纸片，使点A落在EF上的N处，并使折痕经过点B，得到折痕BM，同时得到线段BN.连结AN，易知△ABN的形状是 ▲ .
论证：如图3，若延长MN交BC于点P，试判定△BMP的形状，请说明理由.
