(沪教版)2022年暑假八年级数学复习巩固专题2 一次函数的图像和性质
试卷更新日期:2022-07-13 类型:复习试卷
一、单选题
-
1. 将直线y=﹣3x沿着x轴向右平移2个单位,所得直线的解析式为( )A、y=﹣3x+2 B、y=﹣3x﹣2 C、y=﹣3x﹣6 D、y=﹣3x+62. 将一次函数y =2x-3的图象沿y轴向上平移3个单位长度后,所得图象的函数表达式为( )A、y=2x B、y=2x-6 C、y=5x-3 D、y= -x-33. 要得到函数y=2x+3的图象,只需将函数y=2x的图象( )A、向左平移3个单位 B、向右平移3个单位 C、向下平移3个单位 D、向上平移3个单位4. 已知一次函数y=kx-1,y随着x的增大而增大,将它向上平移2个单位长度后得到直线y=k1x+b,则下列关于直线y=k1x+b的说法正确的是( )A、经过第一、二、三象限 B、与x轴交于点(1,0) C、与y轴交于点(0,-1) D、y随x的增大而减小5. 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x﹣5上时,线段BC扫过的面积为( ).
 A、80 B、88 C、96 D、1006. 已知点A的坐标为 ,点A关于x轴的对称点 落在一次函数 的图象上,则a的值可以是( )A、-4 B、-5 C、-6 D、-77. 已知y是x的正比例函数,且函数图象经过点 ,则在此正比例函数图象上的点是( )A、 B、 C、 D、8. 如图,正比例函数 ( ≠0)和一次函数 ( ≠0)的图象相交于点A(1,1),则不等式 的解集是( )
A、80 B、88 C、96 D、1006. 已知点A的坐标为 ,点A关于x轴的对称点 落在一次函数 的图象上,则a的值可以是( )A、-4 B、-5 C、-6 D、-77. 已知y是x的正比例函数,且函数图象经过点 ,则在此正比例函数图象上的点是( )A、 B、 C、 D、8. 如图,正比例函数 ( ≠0)和一次函数 ( ≠0)的图象相交于点A(1,1),则不等式 的解集是( ) A、 B、 C、 <1 D、 >19. 如图,在同一直角坐标系中,一次函数y=kx+3与反比例函数 的图象位置可能是( )A、
A、 B、 C、 <1 D、 >19. 如图,在同一直角坐标系中,一次函数y=kx+3与反比例函数 的图象位置可能是( )A、 B、
B、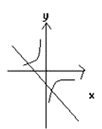 C、
C、 D、
D、 10. 与直线y=﹣4x+2平行的直线是( )A、y=4x+2 B、y=﹣4x+3 C、y D、y
10. 与直线y=﹣4x+2平行的直线是( )A、y=4x+2 B、y=﹣4x+3 C、y D、y二、填空题
-
11. 将直线y=﹣2x向上平移1个单位长度,平移后直线的解析式为 .12. 将直线y=3x向上平移3个单位,得到直线 .13. 如图是一次函数的图象,则关于x的不等式的解集为.
 14. 若直线的图像过点 , 则 .15. 已知一次函数图象经过 , , 则函数表达式为.
14. 若直线的图像过点 , 则 .15. 已知一次函数图象经过 , , 则函数表达式为.三、解答题
-
16. 已知一次函数图象过点(1,4)和(0,2),求这个一次函数的解析式,并在直角坐标系中画出该函数图象.17. 已知一次函数y=kx+b的图象经过点(-2,6),且与直线y=2x平行,求该一次函数的解析式.18. 在直角坐标系中,说明三点A(﹣3, ),B(4,4),C(6,5)在同一直线上.19. 在平面直角坐标系中,直线AB经过(1,1)、(-3,5)两点。来直线AB所对应的两数解析式。
