（沪教版）2022年暑假七年级数学复习巩固专题11 等腰三角形
试卷更新日期：2022-07-13 类型：复习试卷
一、单选题
-
1. 如图，在△ABC中，AB＝AC，BE＝CD，BD＝CF，若∠EDF＝48°，则∠A的度数为（ ）
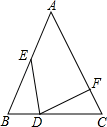A、48 B、64° C、68° D、842. 如图，在△ABC中，∠ABC=50°，∠ACB=100°，点M是射线AB上的一个动点，过点M作MN∥BC交射线AC于点N，连结BN。若△BMN中有两个角相等，则∠MNB的度数不可能是（ ）
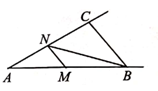A、25° B、30° C、50° D、65°3. 已知一个等腰三角形的周长为22cm，若其中一边长为6cm，则它的腰长为（ ）A、6cm B、10cm C、6cm或8cm D、8cm或10cm4. 如图，下列4个三角形中，均有AB=AC，则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是（ ）
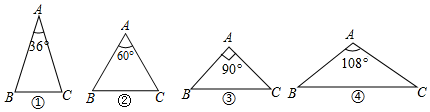A、①②④ B、②③④ C、①②③ D、①③④5. 已知a、b、c是 的三条边，且满足 ，则 是（ ）A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形6. 如图，在△ABC中，AB＝AC，∠A＝36°，BD分别是△ABC的角平分线，则图中的等腰三角形共有（ ）
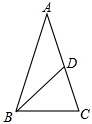A、1个 B、2个 C、3个 D、4个7. 下列三角形中，等腰三角形的个数是（ ）
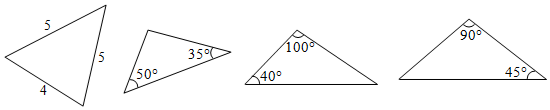A、4个 B、3个 C、2个 D、1个8. 下列条件中，不能判断是等边三角形的是（ ）．A、 ， B、 ， C、 D、9. 如图，P是等边三角形ABC内的一点，且PA=3，PB=4，PC=5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论错误的是（ ）
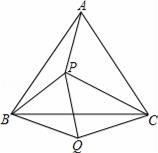A、△BPQ是等边三角形 B、△PCQ是直角三角形 C、∠APB=150° D、∠APC=135°10. 如图，已知∠MON及其边上一点A．以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C．再以点C为圆心，AC长为半径画弧，恰好经过点B．错误的结论是（ ）
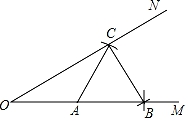A、S△AOC＝S△ABC B、∠OCB＝90° C、∠MON＝30° D、OC＝2BC二、填空题
-
11. 等腰三角形的周长为 ， 若有一边长为 ， 则等腰三角形的其他两边长分别是.12. 若等腰三角形的两边长分别为4和8，则它的周长为.13. 如图，在四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC，CD上分别找一点M，N，使三角形AMN周长最小时，则∠MAN的度数为.
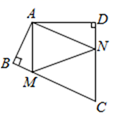14. 如图，已知在 中，AB=AC，点D在边BC上，要使BD=CD，还需添加一个条件，这个条件是 ．（只需填上一个正确的条件）
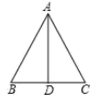15. 如图，将边长为4个单位的等边沿边向右平移3个单位得到 ， 则的长度为.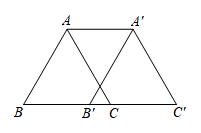
三、解答题
-
16. 如图，已知在中，点D在边上， ， 过点D作交边于点E，请说明的理由．
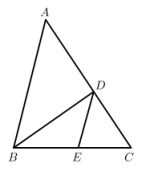17. 如图，在△ABC中，AB＝AC，点D是BC的中点，点E在AB上，BE＝BD，∠BAC＝76°，求∠ADE的大小.
18. 如图，在△ABC中，AB＝AC，点D，E分别是BC，AC上的点，且BD＝CE，连接AD，DE，若∠ADE＝∠B.求证：AD＝DE.（每行都要写理由）
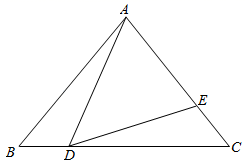19. 如图，已知在△ABC中，AC＝BC＝AD，∠CDE＝∠B，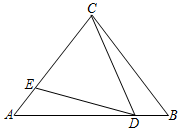
求证：△CDE是等腰三角形．
20. 已知：如图，在△BAC中，AB=AC，D，E分别为AB，AC边上的点，且DE∥BC，求证：△DAE是等腰三角形．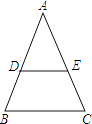
21. 如图，已知O是等边三角形ABC内一点，D是线段BO延长线上一点，且OD＝OA，∠AOB＝120°，求∠BDC的度数．
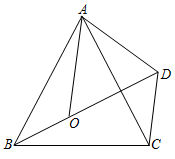22. 如图，已知△ABC，分别以AB、AC为边在△ABC的外部作等边三角形ABD和等边三角形ACE联结DC、BE试说明DC=BE的理由．
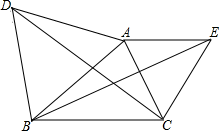23. 已知：如图△ABC是等边三角形，D，E分别是BC，AC上两点且BD=CE，以AD为边在AC一侧作等边△ADF．求证：EF∥BC．
24. 阅读下列材料，解答问题：定义：线段AD把等腰三角形ABC分成△ABD与△ACD（如图1），如果△ABD与△ACD均为等腰三角形，那么线段AD叫做△ABC的完美分割线.
(1)、如图1，已知△ABC中，AB=AC，∠BAC=108°，AD为△ABC的完美分割线，且BD<CD，则∠B= ， ∠ADC=.(2)、如图2，已知△ABC中，AB=AC，∠A=36°，BE为△ABC的角平分线，求证：BE为△ABC完美分割线.(3)、如图3，已知△ABC是一等腰三角形纸片，AB=AC，AD是它的一条完美分割线，将△ABD沿直线AD折叠后，点B落在点B1处，AB1交CD于点E，求证：DB1=EC.