（沪教版）2022年暑假七年级数学复习巩固专题9 平行线

试卷更新日期：2022-07-13 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列条件能判断AB $∥$ CD的是（）

A、∠B =∠D B、∠B +∠DA B=180^° C、∠DAC=∠BCA D、∠B +∠D C B=180^°

查看试题解析
2. 如图，点E在CD的延长线上，BE与AD交于点F下列条件能判断BC∥∥AD的是（）

A、∠1=∠3 B、∠A+∠CDA=180° C、∠4=∠A D、∠2+∠5= 180°

查看试题解析
3. 如图，下列条件能判定DE∥BC的是（）

A、∠1=∠4 B、∠2=∠1 C、∠3=∠CDE D、∠A+∠AEF= 180°

查看试题解析
4. 如图，四边形 $A B C D$ 中，点 $E$ 在 $A B$ 延长线上，则下列条件中不能判断 $A B ∥ C D$ 的是（）

A、 $∠ 5 = ∠ C$ B、 $∠ 1 = ∠ 2$ C、 $∠ 3 = ∠ 4$ D、 $∠ 1 + ∠ 3 + ∠ A = 18 0^{∘}$

查看试题解析
5. 如图，直线 $a$ 、 $b$ 被第三条直线所藏，下列条件不能判断 $a / / b$ 的是（）.

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 + ∠ 1 = 180 °$ C、 $∠ 1 = ∠ 4$ D、 $∠ 2 = 79 °$ ， $∠ 3 = 101 °$

查看试题解析
6. 将一个直角三角板和一把直尺按如图所示的方式摆放，若∠2=55°，则∠1的度数为（）

A、 $45 °$ B、 $55 °$ C、 $25 °$ D、 $35 °$

查看试题解析
7. 如图，将一条两边沿互相平行的纸带折叠．若 $∠ 1 ： ∠ 2 = 4 ： 3$ ，则 $∠ 3$ 的度数是（）

A、100° B、105° C、108° D、144°

查看试题解析
8. 如图，a∥b，M、N分别在a，b上，P为两平行线间一点，那么，∠1+∠2+∠3＝（）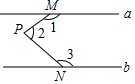

A、180° B、270° C、360° D、540°

查看试题解析
9. 如图，直线a与直线b被直线c所截，b⊥c，垂足为点A，∠1 = 60°，若使直线b与直线a平行，则可将直线b绕着点A顺时针旋转（）

A、60° B、40° C、30° D、20°

查看试题解析
10. 如图，把一个长方形的纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若∠AED′ = 50°，则∠EFC等于（）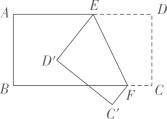

A、65° B、110° C、115° D、130°

查看试题解析

二、填空题

11. 如图， $A B ∥ C D$ ， ∠B=20°，∠D=54°，则∠E为.

查看试题解析
12. 将一张长方形纸条 $A B C D$ 沿 $E F$ 折叠后， $E D$ 与 $B F$ 交于 $G$ 点，若 $∠ E F G = 56 °$ ，则 $∠ B G E$ 的度数是．

查看试题解析
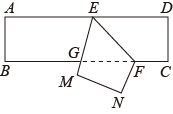13. 如图，点B，C，D在同一条直线上，CE∥AB， $∠ A C B = 9 0^{°}$ ，如果 $∠ E C D = 3 7^{°}$ ，那么 $∠ A =$ ．

查看试题解析
14. 如图所示，∠A=60°，O是AB上一点，直线OD与AB所夹角∠BOD=82°，要使OD∥AC，则直线OD绕点O按逆时针方向至少要旋转度．

查看试题解析
15. 在一副三角尺中∠BPA=45°，∠CPD=60°，∠B=∠C=90°，将它们按如图所示摆放在量角器上，边PD与量角器的0°刻度线重合，边AP与量角器的180°刻度线重合.将三角尺PCD绕点P以每秒3°的速度逆时针旋转，同时三角尺ABP绕点P以每秒2°的速度顺时针旋转，当三角尺PCD的PC边与180°刻度线重合时两块三角尺都停止运动，则当运动时间t =秒时，两块三角尺有一组边平行.

查看试题解析

三、解答题

16. 如图所示，已知∠1是它的补角的3倍，∠2等于它的余角，那么AB//CD吗？为什么？

查看试题解析
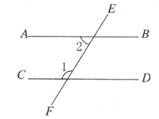17. 在一次数学活动课上，老师让同学们用两个大小、形状都相同的三角板画平行线 $A B$ 、 $C D$ ，并说出自己做法的依据。小琛、小萱、小冉三位同学的做法如下：
小琛说：“我的做法的依据是内错角相等，两直线平行”
小琛说的是否正确？（回答正确或错误）
小萱做法的依据是
小冉做法的依据是．

查看试题解析
18. 如图，已知 $∠ A H F = 130 °$ ， $∠ C G E = 50 °$ ，那么 $A B$ // $C D$ 吗？为什么？

解： $A B$ // $C D$ ．

理由如下：

因为 $∠ A H F + ∠ A H E = 180 °$ （ ▲ ），

又因为 $∠ A H F = 130 °$ （已知），

所以 $∠ A H E = 180 ° - ∠ A H F = 180 ° - 130 ° = 50 °$ （等式性质）．

因为 $∠ C G E = 50 °$ （已知），

得 $∠ C G E = ∠ A H E$ （ ▲ ）．

所以 $A B$ // $C D$ （ ▲ ）．

查看试题解析
19. 如图，已知 $∠ 1 = ∠ 2$ ， $∠ 3 + ∠ 4 = 180 °$ ．求证： $A C / / F G$ ．

证明： $∵ ∠ 1 = ∠ 2$

$∴ A C / /$ ▲ （   ）

$∵ ∠ 3 + ∠ 4 = 180 °$ ，

$∴$ ▲ ∥ ▲ （   ）

$∴ A C / / F G$ （   ）

查看试题解析
20. 如图，直线AB ， CD被直线EF所截，∠1=∠2，求证：AB∥CD；

查看试题解析
21. 按要求完成下列证明：
已知：如图，AB∥CD，直线AE交CD于点C，∠BAC+∠CDF=180° .

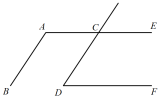
求证：AE∥DF.

证明：∵AB∥CD（   ）

∴∠BAC=∠DCE（   ）

∵∠BAC+∠CDF=180°（已知），

∴    +∠CDF=180°（   ）

∴AE∥DF（   ）.

查看试题解析
22. 完成下面的证明.
如图， $E$ ， $F$ 分别在 $A B$ 和 $C D$ 上， $∠ 1 = ∠ D$ ， $∠ 2$ 与 $∠ C$ 互余， $A F ⊥ C E$ 于点 $G$ .求证 $A B ∥ C D$ .

证明：∵ $A F ⊥ C E$ （已知），

∴ $∠ C G F = 90 °$ （垂直的定义）.

∵ $∠ 1 = ∠ D$ （已知），

∴   ∥   （   ）.

∴ $∠ 4 = ∠ C G F = 90 °$ （   ）.

又∵ $∠ 2 + ∠ C = 90 °$ （已知），

$∠ 2 + ∠ 3 + ∠ 4 =$   （平角的定义），

∴ $∠ 2 + ∠ C = ∠ 2 + ∠ 3 = 90 °$ .

∴ $∠ C =$   .

∴ $A B ∥ C D$ （   ）.

查看试题解析
23. 完成下面推理填空：
如图， $E$ 、 $F$ 分别在 $A B$ 和 $C D$ 上， $∠ 1 = ∠ D$ ， $∠ 2$ 与 $∠ C$ 互余， $A F ⊥ C E$ 于 $G$ ，求证： $A B ∥ C D$ ．
证明：∵ $A F ⊥ C E$
∴ $∠ C G F = 90 °$ （    ）
∵ $∠ 1 = ∠ D$ （已知）
∴                  ▲                   $∥$                   ▲                  （    ）
∴ $∠ 4 = ∠ C G F = 90 °$ （     ）
∵ $∠ 2 + ∠ 3 + ∠ 4 = 180 °$ （平角的定义）
∴ $∠ 2 + ∠ 3 = 90 °$ ．
∵ $∠ 2$ 与 $∠ C$ 互余（已知），
∴ $∠ C = ∠ 3$ （同角的余角相等）
∴ $A B ∥ C D$ （    ）

查看试题解析
24. 如图，已知：EF∥AD，∠1=∠2，∠B=55°，求∠BDG的大小．
请同学们在下面的横线上把解答过程补充完整：
解：∵ EF//AD，（已知）
∴ ∠2=∠3，（           ）
又∵ ∠1=∠2，（已知）
∴ ∠1=∠3，（等量代换）
∴                  ▲                   ，（内错角相等，两直线平行）
∴ ∠B＋∠BDG=180°，（            ）
∵ ∠B=55°，  （已知）
∴ ∠BDG =                  ▲                   ．

查看试题解析