(沪教版)2022年暑假七年级数学复习巩固专题7 垂线
试卷更新日期:2022-07-13 类型:复习试卷
一、单选题
-
1. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则点C到AB的距离是线段( )的长度.
 A、BD B、AD C、CD D、BC2. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )
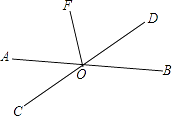
A、BD B、AD C、CD D、BC2. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能正确解释这一现象的数学知识是( )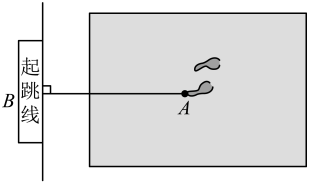 A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直3. 点P为直线外一点,点A、B、C为直线上三点, , , , 则P到直线的距离为( )A、 B、 C、小于 D、不大于4. 如图,OA⊥OB,∠BOC=25°,则∠AOC的度数是( )
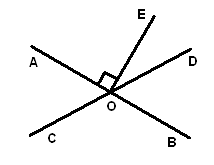
A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直3. 点P为直线外一点,点A、B、C为直线上三点, , , , 则P到直线的距离为( )A、 B、 C、小于 D、不大于4. 如图,OA⊥OB,∠BOC=25°,则∠AOC的度数是( ) A、45° B、55° C、65° D、75°5. 如图,直线AB⊥CD于点O,直线EF经过点O,若∠1=25°,则∠2的度数是( )
A、45° B、55° C、65° D、75°5. 如图,直线AB⊥CD于点O,直线EF经过点O,若∠1=25°,则∠2的度数是( ) A、25° B、65° C、55° D、64°6. 下列说法:①在同一平面内,垂直于同一条直线的两条直线互相平行;②两条直线被第三条直线所截,内错角相等;③如果直线a∥b,b∥c,那么a∥c;④连结直线外一点与直线上各点的所有线段中,垂线段最短;⑤同旁内角的角平分线互相垂直.其中正
A、25° B、65° C、55° D、64°6. 下列说法:①在同一平面内,垂直于同一条直线的两条直线互相平行;②两条直线被第三条直线所截,内错角相等;③如果直线a∥b,b∥c,那么a∥c;④连结直线外一点与直线上各点的所有线段中,垂线段最短;⑤同旁内角的角平分线互相垂直.其中正确的是( )
A、①③④ B、①②⑤ C、②③④ D、②③⑤7. 如图,于C,连接 , 点D是上的动点, , 则点C到点D的最短距离是( ) A、3 B、4 C、 D、8. 如图,P为的边、的垂线的交点, , 则的度数为( )
A、3 B、4 C、 D、8. 如图,P为的边、的垂线的交点, , 则的度数为( ) A、128° B、26° C、38° D、28°9. 如图,直线l1与l2相交于点O,OM⊥l1 , 若β=44°,则a为( )
A、128° B、26° C、38° D、28°9. 如图,直线l1与l2相交于点O,OM⊥l1 , 若β=44°,则a为( ) A、44° B、45° C、46° D、56°10. 如图,在体育课上对学生的立定跳远进行测试,小明从起跳线起跳,点A是小明的脚后跟着地处,过点A作起跳线的垂线,垂足为点B,如图所示.体育老师测得线段AB的长即为小明的跳远成绩,体育老师这样测成绩的依据是( )
A、44° B、45° C、46° D、56°10. 如图,在体育课上对学生的立定跳远进行测试,小明从起跳线起跳,点A是小明的脚后跟着地处,过点A作起跳线的垂线,垂足为点B,如图所示.体育老师测得线段AB的长即为小明的跳远成绩,体育老师这样测成绩的依据是( ) A、两点之间,线段最短 B、两点确定一条直线 C、两点之间距离的定义 D、点到直线的距离的定义
A、两点之间,线段最短 B、两点确定一条直线 C、两点之间距离的定义 D、点到直线的距离的定义二、填空题
-
11. 如图, , , 则表示点到直线所在直线的距离为线段的长度.
 12. 平面直角坐标系中,点 , 若轴,线段的最小值为 .13. 如图,ABCD,平分交于 , , , , 则下列结论:①;②;③;④平分 , 其中正确的是.
12. 平面直角坐标系中,点 , 若轴,线段的最小值为 .13. 如图,ABCD,平分交于 , , , , 则下列结论:①;②;③;④平分 , 其中正确的是. 14. 如图,城建局在河堤上A处向河岸修排水渠时,要求施工人员沿与河岸L垂直的方向开挖,以保证管道铺设最省,这种做法的依据是 。
14. 如图,城建局在河堤上A处向河岸修排水渠时,要求施工人员沿与河岸L垂直的方向开挖,以保证管道铺设最省,这种做法的依据是 。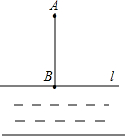 15. 如图,为了方便人们从A点到道路l上,学校过A点作直线l垂线,垂足为B点,这样做的数学原理是 .
15. 如图,为了方便人们从A点到道路l上,学校过A点作直线l垂线,垂足为B点,这样做的数学原理是 .
三、解答题
-
16. 如图,直线AB,CD相交于点O,OE⊥CD于点O,∠EOB=115°,求∠AOC的度数.请补全下面的解题过程(括号中填写推理的依据).

解:∵OE⊥CD于点O(已知),
∴ ▲ ( ▲ ).
∵∠EOB=115°(已知),
∴∠DOB= ▲ =115°-90°=25°.
∵直线AB,CD相交于点O(已知),
∴∠AOC= ▲ =25°( ▲ ).
17. 如图,直线AB与CD相交于点O,EO⊥CD于点O,OF平分∠AOD,且∠BOE=50°.求∠COF的度数. 18. 如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.
18. 如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.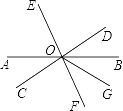 19. 如图,AD⊥BC于点D,EF⊥BC于点F,∠BDG=∠C.试说明∠1=∠2.
19. 如图,AD⊥BC于点D,EF⊥BC于点F,∠BDG=∠C.试说明∠1=∠2. 20. 如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,∠DOB=2∠EOD,求∠AOC,∠COB的度数.
20. 如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,∠DOB=2∠EOD,求∠AOC,∠COB的度数. 21. 如图,直线AB、CD相交于点O,OF⊥CO,∠AOF与∠BOD的度数之比为3:2,求∠AOC的度数.
21. 如图,直线AB、CD相交于点O,OF⊥CO,∠AOF与∠BOD的度数之比为3:2,求∠AOC的度数.