山东省临沂市郯城县2022年九年级数学二模试题
试卷更新日期:2022-07-13 类型:中考模拟
一、单选题
-
1. ( )A、2022 B、-2022 C、 D、2. 如图,直线平分 , 则的度数是( )
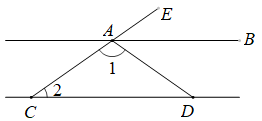 A、 B、 C、 D、3. 若不等式组无解,则a的取值范围为( )A、 B、 C、 D、4. 如图,是放置在北京冬奥会场馆内水平地面上的领奖台,其几何体左视图是( )
A、 B、 C、 D、3. 若不等式组无解,则a的取值范围为( )A、 B、 C、 D、4. 如图,是放置在北京冬奥会场馆内水平地面上的领奖台,其几何体左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 将 进行因式分解,正确的是( )A、 B、 C、 D、6. 如图,在中, , 分别以点A,点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,交AC于D,连接 , 则的长是( )
5. 将 进行因式分解,正确的是( )A、 B、 C、 D、6. 如图,在中, , 分别以点A,点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点O,交AC于D,连接 , 则的长是( ) A、 B、 C、 D、7. 下列运算正确的个数是( )
A、 B、 C、 D、7. 下列运算正确的个数是( )①;②;③;④;⑤;⑥ .
A、1个 B、2个 C、3个 D、4个8. 有两把不同的锁和三把钥匙,其中两把钥匙恰好分别能打开这两把锁,第三把钥匙不能打开这两把锁,任意取出一把钥匙去开任意的一把锁,一次打开锁的概率是( )A、 B、 C、 D、9. 化简的结果是( )A、 B、 C、 D、10. 在分析样本数据时,小华列出了方差的计算公式 , 由公式提供的信息,则下列关于这组样本数据的说法错误的是( )A、样本的容量是3 B、中位数是3 C、众数是3 D、平均数是311. 如图,EF是一个杠杆,可绕支点O自由转动,若动力和阻力的施力方向都始终保持竖直向下,当阻力不变时,则杠杆向下运动时的大小变化情况是( )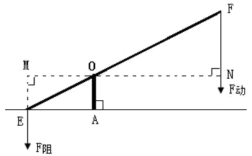 A、越来越小 B、不变 C、越来越大 D、无法确定12. 如图,二次函数的图象与x轴交于A,B两点,与y轴的正半轴交于点C,它的对称轴为直线 . 有下列结论:①;②;③;④当(n为实数)时, , 其中,正确结论的个数是( )
A、越来越小 B、不变 C、越来越大 D、无法确定12. 如图,二次函数的图象与x轴交于A,B两点,与y轴的正半轴交于点C,它的对称轴为直线 . 有下列结论:①;②;③;④当(n为实数)时, , 其中,正确结论的个数是( ) A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
13. 分式方程的解是 .14. 为培养学生动手实践能力,学校七年级生物兴趣小组在项目化学习“制作微型生态圈”过程中,设置了一个圆形展厅.如图,在其圆形边缘上的点P处安装了一台监视器,它的监控角度是50°,为了观察到展厅的每个位置,最少需在圆形边缘上共安装这样的监视器台.
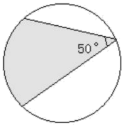 15. 某校举行“停课不停学,名师陪你在家学”活动,计划投资9000元建设几间直播教室,为了保证教学质量,实际每间建设费用增加了20%,并比原计划多建设了两间直播教室,总投资追加了3000元,根据题意,则原计划每间直播教室的建设费用是 .16. 如图,在菱形中,按以下步骤作图:分别以点C和点D为圆心,大于为半径作弧,两弧交于点M,N,作直线 , 且恰好经过点A,与交于点E,连接BE.则下列说法正确的是
15. 某校举行“停课不停学,名师陪你在家学”活动,计划投资9000元建设几间直播教室,为了保证教学质量,实际每间建设费用增加了20%,并比原计划多建设了两间直播教室,总投资追加了3000元,根据题意,则原计划每间直播教室的建设费用是 .16. 如图,在菱形中,按以下步骤作图:分别以点C和点D为圆心,大于为半径作弧,两弧交于点M,N,作直线 , 且恰好经过点A,与交于点E,连接BE.则下列说法正确的是①;②;③若 , 则;④

三、解答题
-
17. 计算:18. 某校要加强中小学生作业、睡眠、手机、读物、体质管理.数学社团成员采用随机抽样的方法,抽取了七年级若干名学生,对他们一周内平均每天的睡眠时间t(单位:h)进行了调查,将数据整理后得到下列不完整的统计图表和扇形统计图:
组别
睡眠时间分组
频数

A
4
B
8
C
m
D
21
E
7
请根据图表信息回答下列问题:
(1)、本次被抽取的七年级学生共有名;(2)、统计图表中,m=;(3)、扇形统计图中,B组所在扇形的圆心角的度数是°;(4)、请估计该校1000名七年级学生中睡眠不足7小时的人数.19. 如图所示,某人通过定滑轮拉动静止在水平面上的箱子,开始时与物体相连的绳和水平面间的夹角为37°,拉动一段距离后,绳与水平面间的夹角为53°,绳子的自由端竖直向下移动了3米,求箱子移动的距离.(绳子伸缩不计)(参考数据:)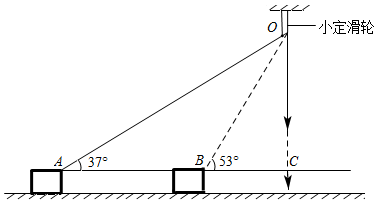 20. 已知函数
20. 已知函数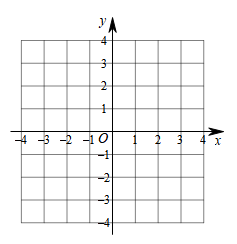 (1)、当时;(2)、已知点在函数图象上,则;(3)、已知函数的图象与函数的图象关于y轴对称,我们称为的镜像函数.请在图中画出 , 的图象.(4)、若直线与函数和的图象有且只有一个交点,则a的取值范围是 .21. 如图,为直径,C、D为上不同于A、B的两点, , 连接CD,过点C作 , 垂足为E,直线与相交于F点.
(1)、当时;(2)、已知点在函数图象上,则;(3)、已知函数的图象与函数的图象关于y轴对称,我们称为的镜像函数.请在图中画出 , 的图象.(4)、若直线与函数和的图象有且只有一个交点,则a的取值范围是 .21. 如图,为直径,C、D为上不同于A、B的两点, , 连接CD,过点C作 , 垂足为E,直线与相交于F点. (1)、求证:为的切线;(2)、当时,求的长.22. 某工厂生产并销售A , B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床 台.(1)、当 时,完成以下两个问题:
(1)、求证:为的切线;(2)、当时,求的长.22. 某工厂生产并销售A , B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床 台.(1)、当 时,完成以下两个问题:①请补全下面的表格:
A型
B型
车床数量/台
▲
每台车床获利/万元
10
▲
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)、当0< ≤14时,设生产并销售A , B两种型号车床获得的总利润为W万元,如何分配生产并销售A , B两种车床的数量,使获得的总利润W最大?并求出最大利润.23. 如图1,在正方形 中,点E是边 上一点,且点E不与点 重合,点F是 的延长线上一点,且 .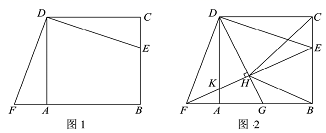 (1)、求证: ;(2)、如图2,连接 ,交 于点K , 过点D作 ,垂足为H , 延长 交 于点G , 连接 .
(1)、求证: ;(2)、如图2,连接 ,交 于点K , 过点D作 ,垂足为H , 延长 交 于点G , 连接 .①求证: ;
②若 ,求 的长.